Data-plus-accessor-object design model

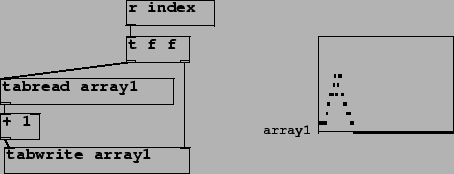
An example of Pd's data-plus-accessor arrangement is that maintained by floating-point arrays (either graphical or via the table object), and the suite of objects tabread, tabwrite, and all their relatives. For example, Figure 3 shows how to use accessor objects to increment a variable element of an array (you would do this to make a histogram of incoming indices, for example.) Here the task is straightforward, and the separation of the storage functionality of the actual ``array1" from the accessor objects is not particularly troublesome.

Figure 3: Incrementing an array element. The receive object can be sent integers to specify which element to increment.

Moving to a more interesting case, we now build a patch to do something corresponding to this using the (still experimental) ``data" feature of Pd [Puc02b]. For completeness we give a short summary here, which will serve also to introduce the central example of this paper.

Pd's ``data" are objects that have a screen appearance; many such objects can be held in one Pd canvas. The canvas holds a linked list of data. A datum belongs to some data structure, which is defined by a patch called a template. The template also defines how the data will look on the page. Lists of data are heterogeneous; a canvas in Pd can hold data with many different structures. Figure 4 shows a canvas with three data objects. They belong to two types: two triangles and one rectangle.

Figure 4: Two data structures in Pd.

As data structures, this list could appear as shown in Figure 5. The elements of the list need not all have the same structure, but they have a ``class" field that determines which of the several possible data structures the element actually belongs to.

Figure 5: Possible structure for the objects in Figure 4.

The data structures are defined by struct objects. Figure 6 shows the struct object corresponding to the triangles in Figure 4. The canvas containing the struct object may also contain drawing instructions such as the drawpolygon object. This object takes three creation arguments to set the interior and border colors and the border width (999, 0, and 2), and then any number of (x, y) pairs to give vertices of the polygon to draw; in this example there are three points and the structure element h gives the altitude of the triangle.

Figure 6: C definitions of the data structure for the triangles in Figure 4.

For clarity, and for the sake of comparison, we'll consider C and Pd approaches to defining and accessing the data in parallel. In C, the definitions of the two data structures might be as shown in Figure 7. In order to be able to mix the two structures in a single linked list, a common structure sits at the head of each. This common structure holds a whichclass field to indicate which structure we're actually looking at, and a next field for holding a collection of these structures in a linked list.

Figure 7: A C equivalent for the data structures of Figure 4.

Now we define a task that might correspond to that of Figure 3. Suppose, given an integer $n$ and a linked list of data structures, we wanted to find the $n$th occurrence of struct1 in the list and increment its h slot. (Note that incrementing the h slot of an instance of class2 wouldn't make sense.) A C function to do this is shown in Figure 8. This is an inherently more complicated problem than that of Figure 3; there, a corresponding piece of C code might simply be:

array[n] += 1;

Instead, we have to make a loop to search through the heterogeneous list, checking each one if it belongs to struct1, maintaining a count, and when all conditions line up, incrementing the h field.

Figure 8: A C function to increment "h" for the nth occurrence of class1.

An equivalent Pd patch is shown in Figure 9. The loop is managed by the until object. The top trigger initializes the f and pointer objects (corresponding to ``count" and ``ptr" in the C code.) The messages, ``traverse pd-list" and ``next", correspond to the initialization and update steps in the C loop; the two possible exit conditions of the loop (the check on ``ptr" and the break in the middle) are the two patchcords reaching back to the right inlet of the until object.

Figure 9: Pd patch to search for the $n$th instance of class1 and increment its value of $h$.

The pointer struct1 object only outputs the pointer if it matches ``struct1" (corresponding to the first if in the C code.) The sel object in the patch corresponds to the check whether ``count" and ``n" are equal in the C code. The remainder, below the second pointer object, is much the same as in Figure 3.