




Next: Audio and control computations
Up: Wavetables and samplers
Previous: Automatic read point precession
Contents
Index
- If a wavetable with
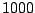 samples is played back at unit transposition,
at a sample rate of 44100 Hertz, how long does the resulting sound last?
samples is played back at unit transposition,
at a sample rate of 44100 Hertz, how long does the resulting sound last?
- A one-second wavetable is played back in 0.5 seconds. By what
interval is the sound transposed?
- Still assuming a one-second wavetable, if we play it back periodically
(in a loop), at how many Hertz should we loop the wavetable to transpose the
original sound upward one half-step?
- We wish to play a wavetable (recorded at
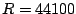 ), looping ten times
per second, so that the original sound stored in the wavetable is transposed up
a perfect fifth (see Page
), looping ten times
per second, so that the original sound stored in the wavetable is transposed up
a perfect fifth (see Page ![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) ). How large a segment of the
wavetable, in samples, should be played back?
). How large a segment of the
wavetable, in samples, should be played back?
- Suppose you wish to use waveform stretching on a wavetable that holds a
periodic waveform of period 100. You wish to hear the untransposed spectrum at
a period of 200 samples. By what duty factor should you squeeze the waveform?
- The first half of a wavetable contains a cycle of a sinusoid of peak
amplitude one. The second half contains zeros. What is the strength of the
second partial of the wavetable?
- A sinusoid is stored in a wavetable with period 4 so that the first four
elements are 0, 1, 0, and -1, corresponding to indices 0, 1, 2, and 3. What
value do we get for an input of 1.5: (a) using 2-point interpolation? (b)
using 4-point interpolation? (c) What's the value of the original sinusoid
there?
- If a wavetable's contents all fall between -1 and 1 in value, what is the
range of possible outputs of wavetable lookup using 4-point interpolation?





Next: Audio and control computations
Up: Wavetables and samplers
Previous: Automatic read point precession
Contents
Index
Miller Puckette
2006-12-30