The sampling theorem

So far we have discussed digital audio signals as if they were capable of describing any function of time, in the sense that knowing the values the function takes on the integers should somehow determine the values it takes between them. This isn't really true. For instance, suppose some function $f$ (defined for real numbers) happens to attain the value 1 at all integers:

$$f(n) = 1 \, , \, \, \, \, \, n = \, \, \ldots, -1, 0, 1, \ldots$$

We might guess that $f(t)=1$ for all real $t$. But perhaps $f$ happens to be one for integers and zero everywhere else--that's a perfectly good function too, and nothing about the function's values at the integers distinguishes it from the simpler $f(t)=1$. But intuition tells us that the constant function is in the spirit of digital audio signals, whereas the one that hides a secret between the samples isn't. A function that is ``possible to sample" should be one for which we can use some reasonable interpolation scheme to deduce its values on non-integers from its values on integers.

It is customary at this point in discussions of computer music to invoke the famous Nyquist theorem. This states (roughly speaking) that if a function is a finite or even infinite combination of sinusoids, none of whose angular frequencies exceeds $\pi$, then, theoretically at least, it is fully determined by the function's values on the integers. One possible way of reconstructing the function would be as a limit of higher- and higher-order polynomial interpolation.

The angular frequency $\pi$, called the Nyquist frequency, corresponds to $R/2$ cycles per second if $R$ is the sample rate. The corresponding period is two samples. The Nyquist frequency is the best we can do in the sense that any real sinusoid of higher frequency is equal, at the integers, to one whose frequency is lower than the Nyquist, and it is this lower frequency that will get reconstructed by the ideal interpolation process. For instance, a sinusoid with angular frequency between $\pi$ and $2\pi$, say $\pi + \omega$, can be written as

$$\cos((\pi + \omega)n + \phi) = \cos((\pi + \omega)n + \phi - 2\pi n)$$

$$= \cos((\omega - \pi)n + \phi)$$

$$= \cos((\pi - \omega)n - \phi)$$

for all integers $n$. (If $n$ weren't an integer the first step would fail.) So a sinusoid with frequency between $\pi$ and $2\pi$ is equal, on the integers at least, to one with frequency between 0 and $\pi$; you simply can't tell the two apart. And since any conversion hardware should do the ``right" thing and reconstruct the lower-frequency sinusoid, any higher-frequency one you try to synthesize will come out your speakers at the wrong frequency--specifically, you will hear the unique frequency between 0 and $\pi$ that the higher frequency lands on when reduced in the above way. This phenomenon is called foldover, because the half-line of frequencies from 0 to $\infty$ is folded back and forth, in lengths of $\pi$, onto the interval from 0 to $\pi$. The word aliasing means the same thing. Figure 3.1 shows that sinusoids of angular frequencies $\pi /2$ and $3\pi /2$, for instance, can't be distinguished as digital audio signals.

Figure 3.1: Two real sinusoids, with angular frequencies $\pi /2$ and $3\pi /2$, showing that they coincide at integers. A digital audio signal can't distinguish between the two.

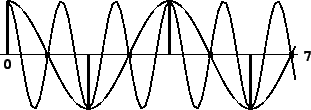We conclude that when, for instance, we're computing values of a Fourier series (Page ), either as a wavetable or as a real-time signal, we had better leave out any sinusoid in the sum whose frequency exceeds $\pi$. But the picture in general is not this simple, since most techniques other than additive synthesis don't lead to neat, band-limited signals (ones whose components stop at some limited frequency). For example, a sawtooth wave of frequency $\omega$, of the form put out by Pd's phasor~ object but considered as a continuous function $f(t)$, expands to:

$$f(t) = {1 \over 2} - {1 \over \pi} { \left ( \sin(\omega ... ...\over 2} + {{\sin(3 \omega t)} \over 3} + \cdots \right ) }$$

which enjoys arbitrarily high frequencies; and moreover the hundredth partial is only 40 dB weaker than the first one. At any but very low values of $\omega$, the partials above $\pi$ will be audibly present--and, because of foldover, they will be heard at incorrect frequencies. (This does not mean that one shouldn't use sawtooth waves as phase generators--the wavetable lookup step magically corrects the sawtooth's foldover--but one should think twice before using a sawtooth wave itself as a digital sound source.)

Many synthesis techniques, even if not strictly band-limited, give partials which may be made to drop off more rapidly than $1/n$ as in the sawtooth example, and are thus more forgiving to work with digitally. In any case, it is always a good idea to keep the possibility of foldover in mind, and to train your ears to recognize it.

The first line of defense against foldover is simply to use high sample rates; it is a good practice to systematically use the highest sample rate that your computer can easily handle. The highest practical rate will vary according to whether you are working in real time or not, CPU time and memory constraints, and/or input and output hardware, and sometimes even software-imposed limitations.

A very non-technical treatment of sampling theory is given in [Bal03]. More detail can be found in [Mat69, pp. 1-30].