 |
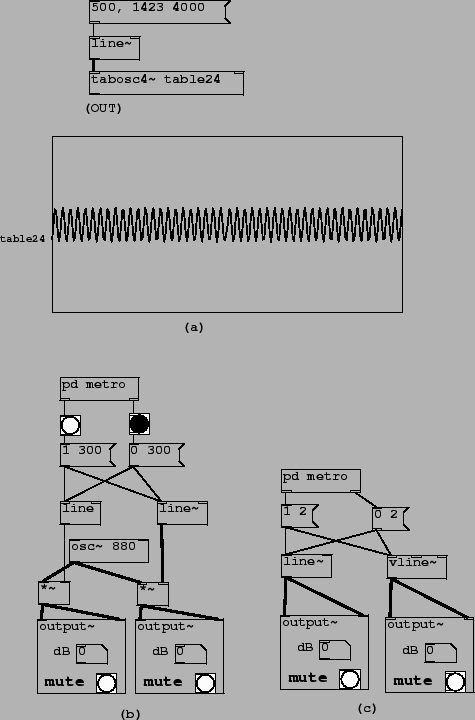
Patch C01.nyquist.pd, shown in Figure 3.13 part (a), shows an oscillator playing a wavetable, sweeping through frequencies from 500 to 1423. The wavetable consists of only the 46th partial, which therefore varies from 23000 to 65458 Hz. At a sample rate of 44100 these two frequencies sound at 21100 and 22742 Hz, but sweeping from one to the other folds down through zero and back up.
Two other waveforms are provided to show the interesting effects of beating between partials which, although they ``should" have been far apart, find themselves neighbors through foldover. For instance, at 1423 Hz, the second harmonic is 2846 Hz whereas the 33rd harmonic sounds at 1423*33-44100 = 2859 Hz--a pronounced dissonance.
Other less extreme examples can still produce audible foldover in less striking
forms. Usually it is still objectionable and it is worth training ones ears to
detect it. Patch C02.sawtooth-foldover.pd (not pictured here) demonstrates this for a sawtooth
(the
![]() object). For wavetables holding audio recordings,
interpolation error can create extra foldover. The effects of this can
vary widely; the sound is sometimes described as
"crunchy" or "splattering", depending on the recording, the transposition,
and the interpolation algorithm.
object). For wavetables holding audio recordings,
interpolation error can create extra foldover. The effects of this can
vary widely; the sound is sometimes described as
"crunchy" or "splattering", depending on the recording, the transposition,
and the interpolation algorithm.