If a sinusoid is given a frequency which varies slowly in time we hear it as having a varying pitch. But if the pitch changes so quickly that our ears can't track the change--for instance, if the change itself occurs at or above the fundamental frequency of the sinusoid--we hear a timbral change. The timbres so generated are rich and widely varying. The discovery by John Chowning of this possibility [Cho73] revolutionized the field of computer music. Here we develop frequency modulation, usually called FM, as a special case of waveshaping [Leb79]; the treatment here is adapted from an earlier publication [Puc01].
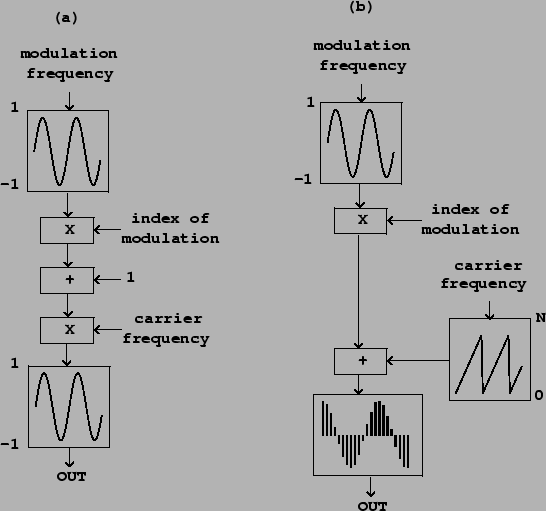
The FM technique, in its simplest form, is shown in figure 5.8
part (a).
A frequency-modulated sinusoid is one whose frequency varies sinusoidally, at
some angular frequency ![]() , about a central frequency
, about a central frequency ![]() , so
that the instantaneous frequencies vary between
, so
that the instantaneous frequencies vary between ![]() and
and
![]() , with parameters
, with parameters ![]() controlling the frequency of
variation, and
controlling the frequency of
variation, and ![]() controlling the depth of variation. The parameters
controlling the depth of variation. The parameters
![]() ,
, ![]() , and
, and ![]() are called the
carrier frequency, the
modulation frequency, and the
index of modulation, respectively.
are called the
carrier frequency, the
modulation frequency, and the
index of modulation, respectively.
It is customary to use a simpler, essentially equivalent formulation in
which the phase, instead of the frequency, of the carrier sinusoid is
modulated sinusoidally. (This gives an equivalent result since the
instantaneous frequency is just the change of phase, and since the
sample-to-sample change in a sinusoid is just another sinusoid.) The
phase modulation formulation is shown in part (b) of the figure.
If the carrier and modulation frequencies don't themselves vary
in time, the resulting signal can be written as
 |
To analyse the resulting spectrum we can write,
Returning to Figure 5.4, we can see at a glance what the
spectrum will look like. The two harmonic spectra, of the waveshaping outputs
Much more about FM can be found in textbooks [Moo90, p. 316] [DJ85] [Bou00] and research publications; some of the possibilities are shown in the following examples.