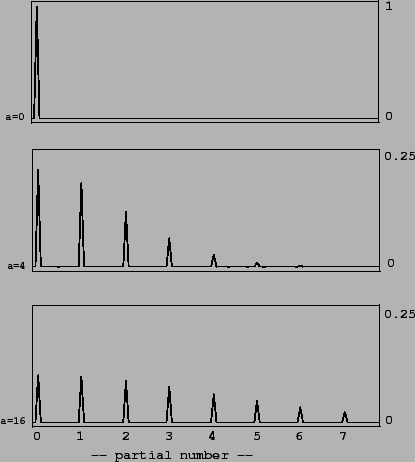
We return now to the spectra computed on Page ![]() ,
corresponding to waveshaping functions of the form
,
corresponding to waveshaping functions of the form ![]() . We note
with pleasure that not only are they all in phase (so that they can
be superposed with easily predictable results) but also that the spectra
spread out increasingly with
. We note
with pleasure that not only are they all in phase (so that they can
be superposed with easily predictable results) but also that the spectra
spread out increasingly with ![]() . Also, in a series of the form,
. Also, in a series of the form,
Now suppose we wish to arrange for different terms in the above expansion
to dominate the result in a predictable way as a function of the index ![]() .
To choose the simplest possible example, suppose we wish
.
To choose the simplest possible example, suppose we wish ![]() to be the largest
term for
to be the largest
term for ![]() , then for it to be overtaken by the more quickly growing
, then for it to be overtaken by the more quickly growing
![]() term for
term for ![]() , which is then overtaken by the
, which is then overtaken by the ![]() term for
term for
![]() and so on, so that the
and so on, so that the ![]() th term takes over at an index equal to
th term takes over at an index equal to ![]() .
To make this happen we just require that
.
To make this happen we just require that
Before plugging in ![]() as a transfer function it's wise to plan how we
will deal with signal amplitude, since
as a transfer function it's wise to plan how we
will deal with signal amplitude, since ![]() grows quickly as a function of
grows quickly as a function of
![]() . If we're going to plug in a sinusoid of amplitude
. If we're going to plug in a sinusoid of amplitude ![]() , the maximum output
will be
, the maximum output
will be ![]() , occuring whenever the phase is zero. A simple and natural
choice is simply to divide by
, occuring whenever the phase is zero. A simple and natural
choice is simply to divide by ![]() to reduce the peak to one, giving:
to reduce the peak to one, giving:
 |