Narrow-band companding

Figure 9.8: Block diagram for narrow-band noise suppression by companding.

A compander is a tool that amplifies a signal with a variable gain, depending on the signal's measured amplitude. The term is a contraction of ``compressor" and ``expander". A compressor's gain increases as the input level increases, so that its dynamic range, that is, the overall variation in signal level, is reduced. An expander does the reverse, increasing the dynamic range. Frequently the gain depends not only on the immediate signal level but on its history; for instance the rate of change might be limited or there might be a time delay.

By using Fourier analysis and resynthesis, we can do companding individually on narrow-band channels. If $C[m]$ is one such band, we apply a gain $g[m]$ to it, to give $g[m]C[m]$. Although $C[m]$ is a complex number, the gain is a non-negative real number. In general the gain could be a function not only of $C[m]$ but also of any or all the previous samples in the channel: $C[m-1]$, $C[m-2]$, and so on. Here we'll consider the simplest situation where the gain is simply a function of the magnitude of the current sample: $\vert C[m]\vert$.

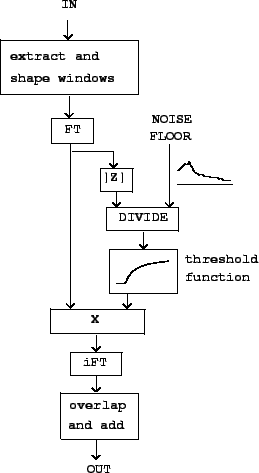
The patch diagrammed in Figure 9.8 shows one very useful application of companding, called a noise gate. Here the gain $g[m]$ depends on the channel amplitude $C[m]$ and a noise floor which is a function $f$ of the channel number $k$. For clarity we will introduce the frequency subscript $k$ to the gain, now written as $g[m, k]$, and to the windowed Fourier transform $S[m, k] = C[m]$. The gain is given by:

$$g[m, k] = \left \{ \begin{array}{ll} {1 - f[k]/\vert S[... ...]\vert > f[k]} \\ 0 & \mbox{otherwise} \end{array} \right .$$

Whenever the magnitude $S[m, k]$ is less than the threshold $f[k]$ the gain is zero and so the amplitude $S[m, k]$ is replaced by zero. When greater, multiplying the amplitude by $g[m, k$ reduces the the magnitude downward to $\vert S[m, k]\vert-f[k]$. Since the gain is a non-negative real number, the phase is preserved.

In the figure, the gain is computed as a thresholding function of the ratio $x = \vert S[m, k]\vert/f[k]$ of the signal amplitude above the noise floor; the threshold is $g(x) = 1-1/x$ when $x<1$ and zero otherwise, although other thresholding functions could easily be substituted.

This technique is useful for removing noise from a recorded sound. We either measure or guess values of $f[k]$ according to a noise floor. Because of the design of the gain function $g[m, k]$, only amplitudes which are above the noise floor reach the output. Since this is done on narrow frequency bands, most of the noise can be removed even while the signal itself, in the frequency ranges where it is louder than the noise floor, is mostly preserved.

This operation is also useful as a pre-processor before applying a non-linear operation, such as distortion, to a sound. It is often best to distort only the most salient frequencies of the sound. Subtracting the noise-gated sound from the original gives a residual signal which can be passed through undistorted.