Phase bashing

In section 2.3 on enveloped sampling we saw how to make a periodic waveform from a recorded sound, thereby borrowing the timbre of the original sound but playing it at a specified pitch. If the window into the recorded sound is made to precess in time, the resulting timbre varies in imitation of the recorded sound.

One important problem arises, which is that if we take waveforms from different windows of a sample (or from different samples), there is no guarantee that the phases of the two match up. If they don't, the result is heard as ugly-sounding frequency deviations (since frequency modulation can be thought of as phase slippage).

Figure 9.13: Phase-bashing a recorded sound (here, a sinusoid with rising frequency) to give a series of oscillator wavetables.

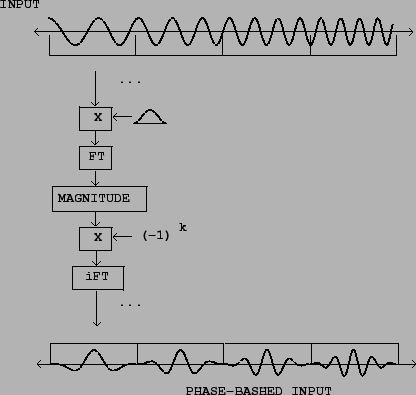
Figure 9.13 shows the simplest way to use Fourier analysis to align phases in a series of windows in a recording. We simply take the FFT of the window and then align the phase so that it is zero for even values of $k$ and $\pi$ for odd ones. The phase at the center of the window is thus zero for both even and off values of $k$. To set the phases (the arguments of the complex amplitudes in the spectrum) in the desired way, first we find the magnitude, which can be considered a complex number with argument zero. Then multiplying by $(-1)^k$ adjusts the amplitude so that it is positive and negative in alternation. Then we take the inverse Fourier transform, without even bothering to window again on the way back; we will probably want to apply a windowing envelope later anyway as was shown in Figure 2.7.