




Next: Wavetables and samplers
Up: Acoustics of digital audio
Previous: conversion between frequency and
Contents
Index
- If 0 dB corresponds to an amplitude of 1,
how many dB corresponds to amplitudes of 1.5, 2, 3, and 5? (Answer:
about 3, 6, 10, and 14.)
- Two uncorrelated signals of RMS amplitude 3 and 4 are added; what's the
RMS amplitude of the sum?
- How many uncorrelated signals, all of equal amplitude, would you have
to add to get a signal that is 9 dB hotter?
- What is the angular frequency of middle C at 44100 samples per second?
- If
![$x[n]$](img74.png) is an audio signal, show that:
is an audio signal, show that:
and
where 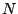 is the window size. Under what conditions does equality hold for
each one?
is the window size. Under what conditions does equality hold for
each one?
- If
![$x[n]$](img74.png) is the SINUSOID of Section 1.1, and making the assumptions
of section 1.2, show that its RMS amplitude is approximately
is the SINUSOID of Section 1.1, and making the assumptions
of section 1.2, show that its RMS amplitude is approximately 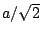 .
Hint: use an integral to approximate the sum. Since the window contains
many periods, you can assume that the integral covers a whole number of periods.
.
Hint: use an integral to approximate the sum. Since the window contains
many periods, you can assume that the integral covers a whole number of periods.





Next: Wavetables and samplers
Up: Acoustics of digital audio
Previous: conversion between frequency and
Contents
Index
Miller Puckette
2005-04-01