Suppose you wish to fade a signal in over a period of ten seconds--that is,
you wish to multiply it by an amplitude-controlling signal ![]() which rises
from 0 to 1 in value over
which rises
from 0 to 1 in value over ![]() samples, where
samples, where ![]() is the sample rate. The
most obvious choice would be a linear ramp:
is the sample rate. The
most obvious choice would be a linear ramp:
![]() . But this will
not turn out to yield a smooth increase in perceived loudness. Over the first
second
. But this will
not turn out to yield a smooth increase in perceived loudness. Over the first
second ![]() rises from
rises from ![]() dB to -20 dB, over the next four by another
14 dB, and over the remaining five, only by the remaining 6 dB. Over most of
the ten second period the rise in amplitude will be barely perceptible.
dB to -20 dB, over the next four by another
14 dB, and over the remaining five, only by the remaining 6 dB. Over most of
the ten second period the rise in amplitude will be barely perceptible.
Another possibility would be to ramp ![]() exponentially, so that it rises
at a constant rate in dB. You would have to fix the initial amplitude to be
inaudible, say 0 dB (if we fix unity at 100 dB). Now we have the opposite
problem: for the first five seconds the amplitude control will rise from
0 dB (inaudible) to 50 dB (pianissimo); this amount of rise should have only
taken up the first second or so.
exponentially, so that it rises
at a constant rate in dB. You would have to fix the initial amplitude to be
inaudible, say 0 dB (if we fix unity at 100 dB). Now we have the opposite
problem: for the first five seconds the amplitude control will rise from
0 dB (inaudible) to 50 dB (pianissimo); this amount of rise should have only
taken up the first second or so.
The natural progression should perhaps have been: 0-ppp-pp-p-mp-mf-f-ff-fff, so that each increase of one dynamic marking would take roughly one second, and would correspond to one "step" in loudness.
We appear to need some scale in between logarithmic and linear. A somewhat
arbitrary choice, but useful in practice, is the quartic curve:
Figure 4.3 shows three amplitude transfer functions:
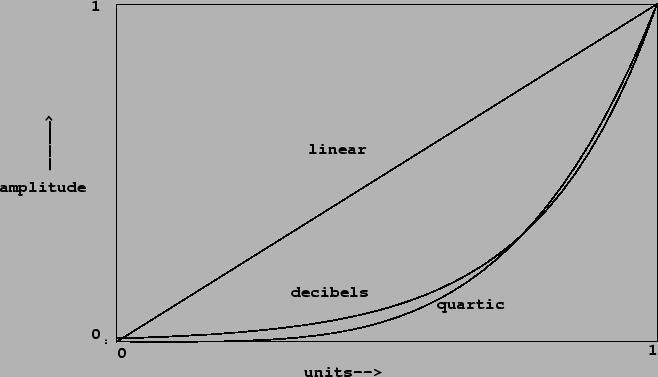 |
We can think of the three curves as showing
transfer functions, from an abstract control (ranging from 0 to 1) to a
linear amplitude. After we choose a suitable transfer function ![]() , we
can compute a corresponding amplitude control signal; if we wish to ramp
over
, we
can compute a corresponding amplitude control signal; if we wish to ramp
over ![]() samples from silence to unity gain, the control signal would be:
samples from silence to unity gain, the control signal would be: