




Next: Parabolic wave
Up: Fourier series of the
Previous: Fourier series of the
Contents
Index
First we apply this to the sawtooth wave ![$s[n]$](img1336.png) . For
. For 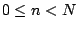 we have:
we have:
Ignoring the DC offset of 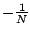 , this gives an
impulse,
zero everywhere except one sample per cycle. The summation in
the Fourier transform only has one term, and we get:
, this gives an
impulse,
zero everywhere except one sample per cycle. The summation in
the Fourier transform only has one term, and we get:
We then apply the difference formula backward to get:
valid for integer values of 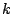 with
with 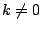 and
and 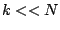 . (To get the second
form of the expression we plugged in
. (To get the second
form of the expression we plugged in
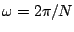 and
and 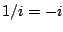 .)
.)
This analysis doesn't give us the DC component
![${\cal FT}\{ s[n] \}(0)$](img1345.png) ,
because we would have had to divide by
,
because we would have had to divide by 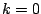 . Instead, we can evaluate the DC
term directly as the sum of all the points of the waveform: it's approximately
zero by symmetry.
. Instead, we can evaluate the DC
term directly as the sum of all the points of the waveform: it's approximately
zero by symmetry.
To get a Fourier series in terms of familiar real-valued sine and cosine functions,
we combine corresponding terms for negative and positive values of 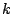 . The
first harmonic (
. The
first harmonic (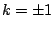 ) is:
) is:
and similarly for other values of 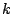 , the
, the 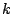 th harmonic is
th harmonic is
and the entire Fourier series is:





Next: Parabolic wave
Up: Fourier series of the
Previous: Fourier series of the
Contents
Index
Miller Puckette
2006-03-03
![]() ,
because we would have had to divide by
,
because we would have had to divide by ![]() . Instead, we can evaluate the DC
term directly as the sum of all the points of the waveform: it's approximately
zero by symmetry.
. Instead, we can evaluate the DC
term directly as the sum of all the points of the waveform: it's approximately
zero by symmetry.
![]() . The
first harmonic (
. The
first harmonic (![]() ) is:
) is: