




Next: General (non-symmetric) triangle wave
Up: Fourier series of the
Previous: Parabolic wave
Contents
Index
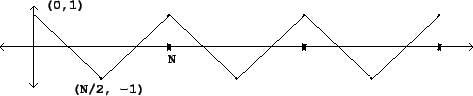
Figure 10.6:
Symmetric triangle wave, obtained by superposing parabolic waves with
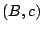 pairs equal to
pairs equal to 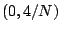 and
and 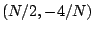 .
.
 |
To demonstrate how to obtain Fourier series for classical waveforms in general,
consider first the square wave,
equal to 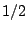 for the first half cycle (
for the first half cycle (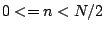 ) and
) and 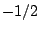 for the rest.
We get the Fourier series by plugging in the Fourier series for
for the rest.
We get the Fourier series by plugging in the Fourier series for ![$s[n]$](img1336.png) twice:
twice:
The symmetric triangle wave (Figure 10.6) given by
similarly comes to
Miller Puckette
2006-03-03

