




Next: Wavetables and samplers
Up: Sinusoids, amplitude and frequency
Previous: More additive synthesis
Contents
Index
- A sinusoid (page
![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) ) has initial phase
) has initial phase 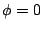 and
angluar frequency
and
angluar frequency
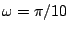 . What is its period in samples? What is
the phase at sample number
. What is its period in samples? What is
the phase at sample number 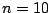 ?
?
- Two sinusoids have periods of 20 and 30 sample, respectively. What is
the period of the sum of the two?
- If 0 dB corresponds to an amplitude of 1,
how many dB corresponds to amplitudes of 1.5, 2, 3, and 5?
- Two uncorrelated signals of RMS amplitude 3 and 4 are added; what's the
RMS amplitude of the sum?
- How many uncorrelated signals, all of equal amplitude, would you have
to add to get a signal that is 9 dB greater in amplitude?
- What is the angular frequency of middle C at 44100 samples per second?
- Two sinusoids play at middle C (MIDI 60) and the neighboring C sharp
(MIDI 61). What is the difference, in Hertz, between their frequuencies?
- How many cents is the interval between the seventh and the eighth harmonic of
a periodic signal?
- If an audio signal
![$x[n], n = 0, ..., M-1$](img163.png) has peak amplitude 1, what
is the minimum possible RMS amplitude? What is the maximum possible?
has peak amplitude 1, what
is the minimum possible RMS amplitude? What is the maximum possible?
- If
![$x[n]$](img79.png) is the sinusoid of page
is the sinusoid of page ![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) , and making
the assumptions of section 1.2, show that its RMS amplitude is approximately
, and making
the assumptions of section 1.2, show that its RMS amplitude is approximately
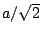 . Hint: use an integral to approximate the sum. Since
the window contains many periods, you can assume that the integral covers a
whole number of periods.
. Hint: use an integral to approximate the sum. Since
the window contains many periods, you can assume that the integral covers a
whole number of periods.





Next: Wavetables and samplers
Up: Sinusoids, amplitude and frequency
Previous: More additive synthesis
Contents
Index
Miller Puckette
2006-09-05