Two recirculating filters for the price of one

When pairing recirculating elementary filters, it is possible to avoid computing one of each pair, as long as the input is real-valued (and so, the output is as well.) Supposing the input is a real sinusoid of the form:

$$A{Z^n} + \overline{A}{Z^{-n}}$$

and we apply a single recirculating filter with coefficient 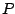$P$. Letting $a[n]$ denote the real part of the output, we have:

$$a[n] = 2 \mathrm{re} \left[ { {1 \over {1 - {P}{Z^{-1}}}}... ...n} + {1 \over {1 - {P}{Z}}} \overline{A}{Z^{-n}}} } \right ]$$

$$= 2 \mathrm{re} \left[ { {1 \over {1 - {P}{Z^{-1}}}} {A{Z^n}} + {1 \over {1 - \overline{P}{Z^{-1}}}} {A{Z^n}} } \right ]$$

$$= 2 \mathrm{re} \left[ { {{ 2 - 2 \, \mathrm{re} (P) {Z^... ...^{-1}}) (1 - {\overline{P}}{Z^{-1}}) }} {A{Z^n}} } \right ]$$

$$= 2 \mathrm{re} \left[ { {{ 1 - \mathrm{re} (P) {Z^{-1}}... ...}}^{-1}}) }} {\overline{A}{{\overline{Z}}^{-n}}} } \right ]$$

(In the second step we used the fact that you can conjugate all or part of an expression, without changing the result, if you're just going to take the real part anyway. The fourth step did the same thing backward.) Comparing the input to the output, we see that the effect of passing a real signal through a complex one-pole filter, then taking the real part, is equivalent to passing the signal through a two-pole, one-zero filter with transfer function equal to:

$${H_{\mathrm{re}}}(Z) = {{ 1 - \mathrm{re} (P) {Z^{-1}} } \over { (1 - {P}{Z^{-1}}) (1 - {\overline{P}}{Z^{-1}}) }}$$

A similar calculation shows that taking the imaginary part (considered as a real signal) is equivalent to filtering the input with the transfer function:

$${H_{\mathrm{im}}}(Z) = {{ \mathrm{im} (P) {Z^{-1}} } \over { (1 - {P}{Z^{-1}}) (1 - {\overline{P}}{Z^{-1}}) }}$$

So taking either the real or imaginary part of a one-pole filter output gives filters with two conjugate poles. The two parts can be combined to synthesize filters with other possible numerators; in other words, with one complex recirculating filter we can synthesize a filter that acts on real signals with two (complex conjugate) poles and one (real) zero.

This technique, known as partial fractions, may be repeated for any number of stages in series as long as we compute the appropriate combination of real and imaginary parts of the output of each stage to form the (real) input of the next stage. No similar shortcut seems to exist for non-recirculating filters; for them it is necessary to compute each member of each complex-conjugate pair explicitly.