Wavetables and samplers

In Chapter 1 we treated audio signals as if they always flowed by in a continuous stream at some sample rate. The sample rate isn't really a quality of the audio signal, but rather it specifies how fast the individual samples should flow into or out of the computer. But audio signals are at bottom just sequences of numbers, and in practice there is no requirement that they be ``played" sequentially. Another, complementary view is that they can be stored in memory, and, later, they can be read back in any order--forward, backward, back and forth, or totally at random. An inexhaustible range of new possibilities opens up.

For many years (roughly 1950-1990), magnetic tape served as the main storage medium for sounds. Tapes were passed back and forth across magnetic pickups to play the signals back in real time. Since 1995 or so, the predominant way of storing sounds has been to keep them as digital audio signals, which are read back with much greater freedom and facility than were the magnetic tapes. Many modes of use dating from the tape era are still current, including cutting, duplication, speed change, and time reversal. Other techniques, such as waveshaping, have come into their own only in the digital era.

Suppose we have a stored digital audio signal, which is just a sequence of samples (i.e., numbers) $x[n]$ for $n = 0, ..., N-1$, where $N$ is the length of the sequence. Then if we have an input signal $y[n]$ (which we can imagine to be flowing in real time), we can use its values as indices to look up values of the stored signal $x[n]$. This operation, called wavetable lookup, gives us a new signal, $z[n]$, calculated as:

$$z[n] = x[y[n]]$$

Schematically we represent this operation as shown in Figure 2.1.

Figure 2.1: Diagram for wavetable lookup. The input is in samples, ranging approximately from 0 to the wavetable's size $N$, depending on the interpolation scheme.

Two complications arise. First, the input values, $y[n]$, might lie outside the range $0, ..., N-1$, in which case the wavetable $x[n]$ has no value and the expression for the output $z[n]$ is undefined. In this situation we might choose to clip the input, that is, to substitute 0 for anything negative and $N-1$ for anything N or greater. Alternatively, we might prefer to wrap the input around end to end. Here we'll adopt the convention that out-of-range samples are always clipped; when we need wraparound, we'll introduce another signal processing operation to do it for us.

The second complication is that the input values need not be integers; in other words they might fall between the points of the wavetable. In general, this is addressed by choosing some scheme for interpolating between the points of the wavetable. For the moment, though, we'll just round down to the nearest integer below the input. This is called non-interpolating wavetable lookup, and its full definition is:

$$z[n] = \left \{ { \begin{array}{ll} x[ \lfloor y[n] \rflo... ...x[N-1] & \mbox{if $y[n] \ge N-1$} \\ \end{array} } \right .$$

(where the symbol $\lfloor y[n] \rfloor$ means, ``the greatest integer not exceeding $y[n]$").

Pictorally, we use $y[0]$ (a number) as a location on the horizontal axis of the wavetable shown in Figure 2.1, and the output, $z[0]$, is whatever we get on the vertical axis; and the same for $y[1]$ and $z[1]$ and so on. The ``natural" range for the input $y[n]$ is $0 \le y[n] < N$. This is different from the usual range of an audio signal suitable for output from the computer, which ranges from -1 to 1 in our units. We'll see later that the usable range of input values, from 0 to $N$ for non-interpolating lookup, shrinks slightly if interpolating lookup is used.

Figure 2.2 (part a) shows a wavetable and the result of using two different input signals as lookup indices into it. The wavetable contains 40 points, which are numbered from 0 to 39. In part (b), a sawtooth wave is used as the input signal $y[n]$. A sawtooth wave is nothing but a ramp function repeated end to end. In this example the sawtooth's range is from $0$ to $40$ (this is shown in the vertical axis). The sawtooth wave thus scans the wavetable from left to right--from the beginning point 0 to the endpoint 39--and does so every time it repeats. Over the fifty points shown in Figure 2.2 (part b) the sawtooth wave makes two and a half cycles. Its period is twenty samples, or in other words the frequency (in cycles per second) is $R/20$.

Figure 2.2: Wavetable lookup: (a) a wavetable; (b) and (d) signal inputs for lookup; (c) and (e) the corresponding outputs.

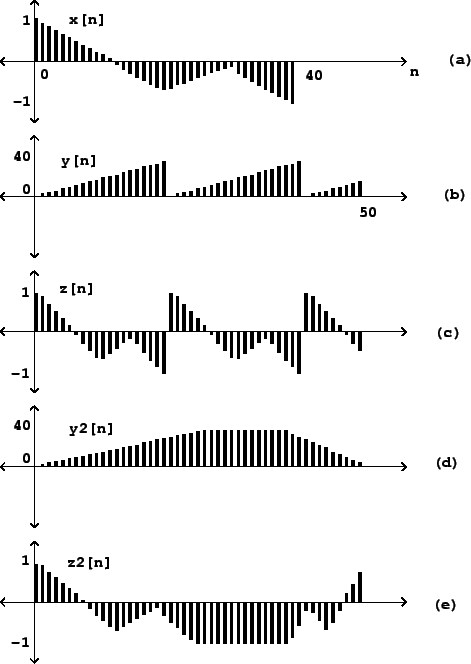Part (c) of Figure 2.2 shows the result of applying wavetable lookup, using the table $x[n]$, to the signal $y[n]$. Since the sawtooth input simply reads out the contents of the wavetable from left to right, repeatedly, at a constant rate of precession, the result will be a new periodic signal, whose waveform (shape) is derived from $x[n]$ and whose frequency is determined by the sawtooth wave $y[n]$.

Parts (d) and (e) show an example where the wavetable is read in a nonuniform way; since the input signal rises from $0$ to $N$ and then later recedes to $0$, we see the wavetable appear first forward, then frozen at its endpoint, then backward. The table is scanned from left to right and then, more quickly, from right to left. As in the previous example the incoming signal controls the speed of precession while the output's amplitudes are those of the wavetable.