




Next: Properties of Fourier transforms
Up: Fourier analysis of periodic
Previous: Periodicity of the Fourier
Contents
Index
Fourier transform as additive synthesis
Now consider an arbitrary signal ![$X[n]$](img669.png) that repeats every
that repeats every 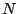 samples. (Previously we
had assumed that
samples. (Previously we
had assumed that ![$X[n]$](img669.png) could be obtained as a sum of sinusoids, and we haven't
yet found out whether every periodic
could be obtained as a sum of sinusoids, and we haven't
yet found out whether every periodic ![$X[n]$](img669.png) can be obtained that way.) Let
can be obtained that way.) Let
![$Y[k]$](img1062.png) denote the Fourier transform of
denote the Fourier transform of 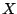 for
for
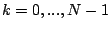 :
:
In the second version we rearranged the exponents to show that ![$Y[k]$](img1062.png) is a sum
of complex sinusoids, with complex amplitudes
is a sum
of complex sinusoids, with complex amplitudes ![$X[m]$](img1067.png) and frequencies
and frequencies 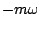 for
for
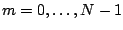 . In other words,
. In other words, ![$Y[k]$](img1062.png) can be considered as a
Fourier series in its own right, whose
can be considered as a
Fourier series in its own right, whose 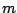 th component has strength
th component has strength ![$X[-m]$](img1070.png) .
(The expression
.
(The expression ![$X[-m]$](img1070.png) makes sense because
makes sense because 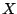 is a periodic signal).
We can also express the amplitude of the partials of
is a periodic signal).
We can also express the amplitude of the partials of ![$Y[k]$](img1062.png) in terms of its own
Fourier transform. Equating the two gives:
in terms of its own
Fourier transform. Equating the two gives:
This means in turn that ![$X[-m]$](img1070.png) can be obtained by summing sinusoids with
amplitudes
can be obtained by summing sinusoids with
amplitudes ![$Y[k]/N$](img1072.png) . Setting
. Setting 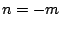 gives:
gives:
This shows that any periodic ![$X[n]$](img669.png) can indeed be obtained as a sum of
sinusoids. Further, the formula explicitly shows how to reconstruct
can indeed be obtained as a sum of
sinusoids. Further, the formula explicitly shows how to reconstruct ![$X[n]$](img669.png) from its Fourier transform
from its Fourier transform ![$Y[k]$](img1062.png) , if we know its value for the integers
, if we know its value for the integers
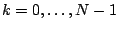 .
.





Next: Properties of Fourier transforms
Up: Fourier analysis of periodic
Previous: Periodicity of the Fourier
Contents
Index
Miller Puckette
2006-12-30
![]() that repeats every
that repeats every ![]() samples. (Previously we
had assumed that
samples. (Previously we
had assumed that ![]() could be obtained as a sum of sinusoids, and we haven't
yet found out whether every periodic
could be obtained as a sum of sinusoids, and we haven't
yet found out whether every periodic ![]() can be obtained that way.) Let
can be obtained that way.) Let
![]() denote the Fourier transform of
denote the Fourier transform of ![]() for
for
![]() :
: