We can use the phase shift formula above to find the Fourier transform of
any complex sinusoid ![]() with frequency
with frequency ![]() , simply by setting
, simply by setting
![]() in the formula and using the Fourier transform for DC:
in the formula and using the Fourier transform for DC:
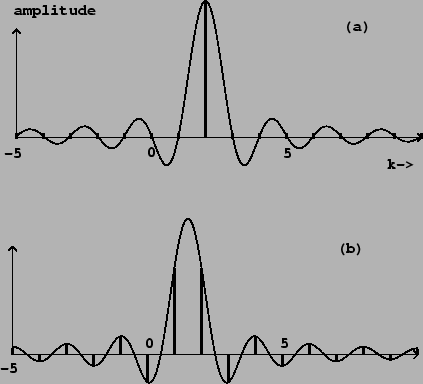 |
If the sinusoid's frequency ![]() is an integer multiple of the fundamental
frequency
is an integer multiple of the fundamental
frequency ![]() , the Dirichlet kernel is shifted to the left or right by an
integer. In this case the zero crossings of the Dirichlet kernel line up with
integer values of
, the Dirichlet kernel is shifted to the left or right by an
integer. In this case the zero crossings of the Dirichlet kernel line up with
integer values of ![]() , so that only one partial is nonzero. This is pictured
in Figure 9.3 (part a).
, so that only one partial is nonzero. This is pictured
in Figure 9.3 (part a).
 |
Part (b) shows the result when the frequency ![]() falls halfway between two
integers. The partials have amplitudes falling off roughly as
falls halfway between two
integers. The partials have amplitudes falling off roughly as ![]() in both
directions, measured from the actual frequency
in both
directions, measured from the actual frequency ![]() . That the energy
should be spread over many partials, when after all we started with a single
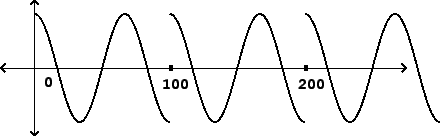
sinusoid, might seem surprising at first. However, as shown in Figure
9.4, the signal repeats at a period
. That the energy
should be spread over many partials, when after all we started with a single
sinusoid, might seem surprising at first. However, as shown in Figure
9.4, the signal repeats at a period ![]() which disagrees with the
frequency of the sinusoid. As a result there is a discontinuity at the
beginning of each period, and energy is flung over a wide range
of frequencies.
which disagrees with the
frequency of the sinusoid. As a result there is a discontinuity at the
beginning of each period, and energy is flung over a wide range
of frequencies.