Miller Puckette 1
On the frequent occasions when one reaches for one or another sort of filter, one can choose either a time-domain ``classical" filter or an FFT-based one. Typically, time-domain ones can achieve very sharp frequency definition and low time latency, and are often cheaper to implement than FFT-based ones. But FFT-based ones have other graces such as explicit phase control and greater ease of varying the filter characteristics in time. Furthermore, certain applications lend themselves naturally to FFT filtering: for example, frequency-band-variable spatialization [Torchia and LippeTorchia and Lippe2003] or delay [Kim-BoyleKim-Boyle2004], or ``vocoders" or ``timbre stamps" in which the spectrum of one sound is used to derive a filter for another [Settel and LippeSettel and Lippe1998] [PuckettePuckette2007].
Here we will consider some issues that arise in FFT-based filtering, particularly for timbre stamping. The following section sets a framework and defines parameters used. Next, we consider whether, and when, FFT filtering really works correctly with arbitrary time-varying filter gains.
In Sections 5 and 6 we turn our attention to the the timbre stamping algorithm. Several possible variations are developed. All of them boil down to computations of various time-varying FFT channel gains, thus fitting into the framework developed and analyzed in Sections 1 through 4.
Using variable names and conventions as in [PuckettePuckette2007], the filters under discussion take an input
signal ![]() , possibly complex-valued, and compute
short-time spectra
, possibly complex-valued, and compute
short-time spectra
| (1) |
![\begin{displaymath}
\equiv
{ \sum _ {n=0} ^ {N-1} {e ^ {- 2 \pi i n k / N}} {w_a}[n]X[n+mH] }
\end{displaymath}](img4.png)
We will use ``linear-phase" filters in which we multiply the spectra by
real-valued gains ![]() , which may depend both on frequency
, which may depend both on frequency ![]() and frame
number
and frame
number ![]() . (For a non-time-varying filter there is no
. (For a non-time-varying filter there is no ![]() dependence so that
we may write the gain as
dependence so that
we may write the gain as ![]() .)
.)
The output is then computed by windowing and overlap-adding the inverse
Fourier transform:
| (2) |
It is reasonable to ask that the signal ![]() be correctly reconstructed when
the filter gains are all 1, which implies:
be correctly reconstructed when
the filter gains are all 1, which implies:
| (3) |
A possible choice for the analysis and resynthesis window function
is the Hann window:
| (4) |
| (5) |
| (6) |
The filter is completely specified by the gains ![]() ,
the window size
,
the window size ![]() , the analysis and resynthesis window functions (including
``squeeze factors"
, the analysis and resynthesis window functions (including
``squeeze factors" ![]() ), and the
overlap, defined as
), and the
overlap, defined as ![]() .
.
Our analysis will loosely follow that given in [AllenAllen1977] and appendix
B of
[Laroche and DolsonLaroche and
Dolson1999].
Assuming the filter is time-invariant (i.e., the gain ![]() does not depend on the
frame number
does not depend on the
frame number ![]() ), we can predict its behavior from that of the low-pass filter
with
), we can predict its behavior from that of the low-pass filter
with ![]() and
and ![]() for
for ![]() . This is possible because, first,
the filter's output is a linear function of
. This is possible because, first,
the filter's output is a linear function of ![]() , and second, passing a
signal through a filter admitting
only the
, and second, passing a
signal through a filter admitting
only the ![]() bin gives the same results as for the zeroth bin,
except with a frequency shift.
bin gives the same results as for the zeroth bin,
except with a frequency shift.
Suppose we introduce the sinusoid ![]() with angular
frequency
with angular
frequency ![]() and whose frequency in bins is
and whose frequency in bins is
![]() . The Fourier transform at DC is
. The Fourier transform at DC is
| (7) |
We now take the inverse FT and overlap-add using the resynthesis window
function. Viewed in the time domain, this convolves the resynthesis window
function with the signal:
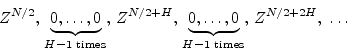 |
(8) |
| (9) |
| (10) |
| (11) |
The signal is attenuated at the analysis stage by
![]() , and
again at the resynthesis stage by
, and
again at the resynthesis stage by
![]() , so the frequency
response is the product of the magnitudes of the two. If we use Hann windows
with no squeezing, we get 12 dB reduction at
, so the frequency
response is the product of the magnitudes of the two. If we use Hann windows
with no squeezing, we get 12 dB reduction at ![]() and 2.84 at
and 2.84 at ![]() ;
so the bandwidth can reasonably be stated as one bin. But if, for example,
we wish to
place a filter at a center frequency of
;
so the bandwidth can reasonably be stated as one bin. But if, for example,
we wish to
place a filter at a center frequency of ![]() , we have to
superpose filters at
, we have to
superpose filters at ![]() and
and ![]() . The gain then only falls
off 1.9 dB one half bin off peak and 5.7 dB one bin off (at
. The gain then only falls
off 1.9 dB one half bin off peak and 5.7 dB one bin off (at ![]() , e.g.).
If desired, the uniformity of bandwidth can be improved by zero-padding the
Fourier transforms, effectively doubling
, e.g.).
If desired, the uniformity of bandwidth can be improved by zero-padding the
Fourier transforms, effectively doubling ![]() and using squeeze factors of 0.5
so that the filter may be expressed at a resolution of
and using squeeze factors of 0.5
so that the filter may be expressed at a resolution of ![]() bin instead of 1.
bin instead of 1.
The low-pass filter (from which we may understand the behavior of any other
filter) may be made time-varying by specifying that the gain ![]() be
zero except when
be
zero except when ![]() , but varying with
, but varying with ![]() . Since the filter output is a
linear function of the gain
. Since the filter output is a
linear function of the gain ![]() , it suffices to know the behavior of a
sinusoidally varying filter:
, it suffices to know the behavior of a
sinusoidally varying filter:
| (12) |
Everything goes as before and out come the frequencies:
| (13) |
| (14) |
As before, the transfer function is the product of the two window functions, but
the resynthesis window function acts at the aliased frequency; the frequency
response is equal to
![]() . If we wish,
therefore, for the frequency response to behave ``properly", that is, as a
function of
. If we wish,
therefore, for the frequency response to behave ``properly", that is, as a
function of ![]() alone, we should squeeze the resynthesis window so that its
larger bandwidth makes the frequency response less dependent on
alone, we should squeeze the resynthesis window so that its
larger bandwidth makes the frequency response less dependent on ![]() . This
can be done only at the expense of raising the minimum attainable bandwidth.
. This
can be done only at the expense of raising the minimum attainable bandwidth.
Figure 1 shows an overall block diagram for the timbre stamp. The three operations at left are the analysis/resynthesis chain of Section 1, with the input now renamed ``FILTER INPUT" to distinguish it from a new, second input that alters the filter. The filter input passes first through a windowed short-time Fourier transform (WSTFT), whose outputs are complex-valued. These are multiplied by a real-valued gain (i.e., their magnitudes are changed but their phases maintained). Then the output is computed using a windowed short-time inverse Fourier transform (WSTIFT).
The gain is a function of the magnitudes of two spectra: that of the original input and that of a second, ``control" input. In the simplest procedure we would simply compute the ratio of the control amplitude to the original amplitude (individually for each bin) so that the gain multiplication replaces the original amplitude with the new one; but there are many possible refinements as discussed below.
In light of the previous discussion of allowable bandwidth of the filter
coefficients, we can now make preliminary bounds on overlap and squeeze
factors. We'll continue to assume squeezed Hann windows so that the windowing
bandwidth is ![]() bins. If we consider the gain computation as being
approximated by a polynomial function of the two spectra (the complex
amplitudes and their conjugates, say, so that the square magnitude is of degree
two), then terms of degree
bins. If we consider the gain computation as being
approximated by a polynomial function of the two spectra (the complex
amplitudes and their conjugates, say, so that the square magnitude is of degree
two), then terms of degree ![]() will yield at most frequencies of
will yield at most frequencies of ![]() where
where
![]() is the minimum (i.e., worse case) of the squeeze factors of the two
analysis windows. To control terms up to degree
is the minimum (i.e., worse case) of the squeeze factors of the two
analysis windows. To control terms up to degree ![]() , we must choose an
overlap factor
, we must choose an
overlap factor ![]() of at least
of at least
| (15) |
Figure 2 shows a block diagram for computing an appropriate gain for the timbre stamp, including several possible variations that are useful at times. The main idea is simply to divide the two spectra bin by bin, returning the quotient in linear amplitude units. The two inputs are assumed to be in units of power (squared amplitude). The operations labeled ``convolve" and ``squelch", and the division, may be carried out in those units. The next operation (``depth" control) is best carried out in so-called Sones [Rossing, Moore, and WheelerRossing et al.2002, p. 108], which we here approximate as square root of amplitude (fourth root of power). Finally, if needed, a low-pass filter may be added to control foldover; it should be applied to the gain expressed in linear amplitude units.
The first, ``convolve" operation in effect averages neighboring power measurements in order to prevent peaks arising from the filter input from falling between neighboring, relevant peaks in the control signal [PenrosePenrose2001]. This may also help in averaging out interference patterns between peaks of the incoming signals.
At frequency bands in which the filtering signal has very low level, it might give unfortunate results to divide by its power spectrum. For this reason it is usually wise to put some sort of limit on the gain that will be applied when filtering it. There are two places in the chain where this might be done. The most logical-sounding spot is after computing the gain as a quotient of the two power spectra. This control appears as ``max gain" in the block diagram. Gains greater than a fixed threshold are simply limited to that threshold.
An alternative viewpoint is to regard the filter as having two stages, the first in which the filtering signal is ``whitened" by dividing by its own amplitude (so that the resulting spectrum has equal energy at all frequencies), and then applying the spectrum of the control signal as a further stage. It often yields good results to limit the gain of the ``whitening" stage instead of limiting the quotient of the two gains. This control appears as ``squelch" in the block diagram. Squelching effectively sets a minimum strength below which the filter input is considered silent, by limiting it below before dividing by it. It is often useful to set squelch to decrease as a function of frequency. (All these controls may vary with time and/or frequency as desired).
Another possible control is the ``depth" of the effect. If we consider the identity filter (with unit gain) as one extreme, and fully applying the timbre stamp as the other extreme, then a continuum of mixtures is available between the two. Cross-fading between the two is best done in units of Sones. One can even choose ``depth" values outside the range from zero to one to generate deeper than 100% filtering, or to filter the original input ``away" from the timbre of the control input.
It is possible to morph one sound into another using two timbre stamps applied in opposing directions, with one ``depth" ramped from 0 to 1 and the other from 1 to 0. One then cross-fades from the first timbre stamp to the second one over a suitably chosen sub-interval of the ramping period.
Finally, either to control foldover or as an effect in its own right, one can low-pass filter the filter gains. This can be brought about naturally by increasing the analysis window size (or making the squeeze factor of the control input analysis greater than that of the filtering input), but this also would have the effect of narrowing the analysis bandwidth. If a higher bandwidth is desired one can return to a smaller window size and, in compensation, low-pass filter the filter gains. This is an alternative to the strategy of convolving a suitable kernel into the power spectra at the top of the diagram; each has its own advantages and drawbacks.
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -no_navigation icmc07-reprint
The translation was initiated by on 2007-08-13