The most fundamental property of a digital audio signal is its
amplitude. Unfortunately, a signal's amplitude has no one canonical
definition.
Strictly speaking, all the samples in a digital audio signal are themselves
amplitudes, and we also spoke of the amplitude ![]() of the sinusoid as a whole.
It is useful to have measures
of amplitude for digital audio signals in general. Amplitude
is best thought of as applying to a
window, a fixed range of samples of the signal. For instance, the
window starting at sample
of the sinusoid as a whole.
It is useful to have measures
of amplitude for digital audio signals in general. Amplitude
is best thought of as applying to a
window, a fixed range of samples of the signal. For instance, the
window starting at sample ![]() of length
of length ![]() of an audio signal
of an audio signal ![]() consists of the
samples,
consists of the
samples,
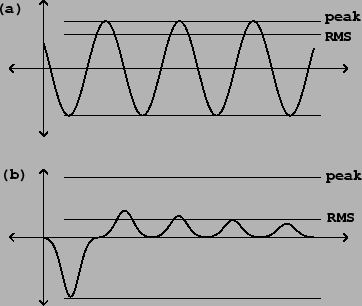
The RMS amplitude of a signal may equal the peak amplitude but never exceeds
it; and it may be as little as ![]() times the peak amplitude, but
never less than that.
times the peak amplitude, but
never less than that.
 |
Under reasonable conditions--if the window contains at least several periods and
if the angular frequency is well under one radian per sample--the peak
amplitude of the sinusoid of Page ![]() is approximately
is approximately ![]() and its RMS amplitude
about
and its RMS amplitude
about ![]() . Figure 1.2 shows the peak and RMS amplitudes
of two digital audio signals.
. Figure 1.2 shows the peak and RMS amplitudes
of two digital audio signals.