 |
The same techniques will work to analyze any delay network, although for more complicated networks it becomes harder to characterize the results, or to design the network to have specific, desired properties. Another point of view can sometimes be usefully brought to the situation, particularly when flat frequency responses are needed, either in their own right or else to ensure that a complex, recirculating network remains stable at feedback gains close to one.
The central fact we will use is that if any delay network, with either one or many inputs and outputs, is constructed so that its output power (averaged over time) always equals its input power, that network has to have a flat frequency response. This is almost a tautology; if you put in a sinusoid at any frequency on one of the inputs, you will get sinusoids of the same frequency at the outputs, and the sum of the power on all the outputs will equal the power of the input, so the gain, suitably defined, is exactly one.
In order to work with power-conserving delay networks we will need an
explicit definition of ``total average power".
If there is only one signal (call it ![]() ), the average power is
given by:
), the average power is
given by:
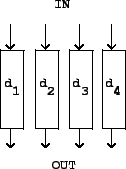
It turns out that a wide range of interesting delay networks has the property that the total power output equals the total power input; they are called unitary. First, we can put any number of delays in parallel, as shown in Figure 7.11. Whatever the total power of the inputs, the total power of the outputs has to be the same.
A second family of power-preserving transformations is composed of rotations and
reflections of the signals ![]() , ... ,
, ... , ![]() , considering them, at
each fixed time point
, considering them, at
each fixed time point ![]() , as
, as ![]() numbers, or as a point in an
numbers, or as a point in an ![]() -dimensional
space. The rotation or reflection must be one that leaves the origin
-dimensional
space. The rotation or reflection must be one that leaves the origin
![]() fixed.
fixed.
For each sample number ![]() , the total
contribution to the average signal power is proportional to
, the total
contribution to the average signal power is proportional to
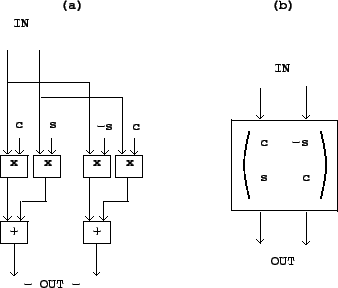 |
Figure 7.12 shows a rotation matrix operating on two signals. In
part (a) the transformation is shown explicitly. If the input signals are
![]() and
and ![]() , the outputs are:
, the outputs are:
For an alternative description of rotation in two dimensions,
consider complex numbers
![]() and
and
![]() . The above transformation amounts to setting
. The above transformation amounts to setting
If we perform a rotation on a pair of signals and then invert one (but not the
other) of them, the result is a
reflection.
This also preserves total signal power, since we can invert any or all of a
collection of signals without changing the total power. In two dimensions, a
reflection appears as a transformation of the form
Special and useful rotation and reflection matrices are obtained by setting the
![]() , so that
, so that
![]() . This
allows us to simplify the computation as shown in Figure 7.13 (part
a) because each signal need only be multiplied by the one quantity
. This
allows us to simplify the computation as shown in Figure 7.13 (part
a) because each signal need only be multiplied by the one quantity ![]() .
.
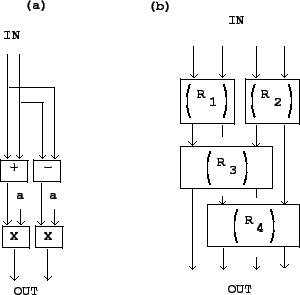 |
Any rotation or reflection of more than two input signals may be accomplished by
repeatedly rotating and/or reflecting them in pairs. For example, in part (b)
of Figure 7.13, four signals are combined in pairs, in two succesive
stages, so that in the end every signal input feeds into all the outputs. We
could do the same with eight signals (using three stages) and so on.
Furthermore, if we use the special angle ![]() , all the input signals will
contribute equally to each of the outputs.
, all the input signals will
contribute equally to each of the outputs.
Any combination of delays and rotation matrices, applied in succession to a collection of audio signals, will result in a flat frequency response, since each individual operation does.
This already allows us to generate an infinitude of flat-response delay networks, but so far, none of them are recirculating. A third operation, shown in Figure 7.14, allows us to make recirculating networks that still enjoy flat frequency responses.
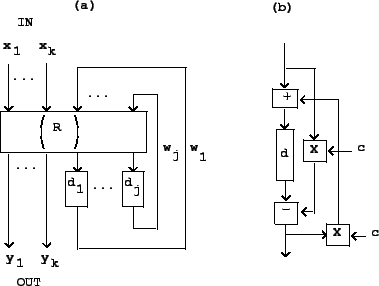 |
Part (a) of the figure shows the general layout. The transformation ![]() is
assumed to be any combination of delays and mixing matrices that are power
preserving in the aggregate. The input signals
is
assumed to be any combination of delays and mixing matrices that are power
preserving in the aggregate. The input signals
![]() are collectively labeled as a compound signal
are collectively labeled as a compound signal ![]() , and
similarly the output signals
, and
similarly the output signals
![]() are shown as
are shown as ![]() . Some
other signals
. Some
other signals
![]() (where
(where ![]() is not necessarily equal to
is not necessarily equal to ![]() )
appear at the output of the transformation
)
appear at the output of the transformation ![]() and are fed back to its input.
and are fed back to its input.
If ![]() is indeed power preserving, the total input power (the power of the
signals
is indeed power preserving, the total input power (the power of the
signals ![]() plus that of the signals
plus that of the signals ![]() ) must equal the output power (the
power of the signals
) must equal the output power (the
power of the signals ![]() plus
plus ![]() ), and subtracting the power of
), and subtracting the power of ![]() from the
equality, we find that the input and the output power are equal.
from the
equality, we find that the input and the output power are equal.
If we let ![]() so that
so that ![]() ,
, ![]() , and
, and ![]() each represent a single signal, and
let the transformation
each represent a single signal, and
let the transformation ![]() be a rotation by
be a rotation by ![]() , followed by a delay of
, followed by a delay of
![]() samples on the
samples on the ![]() output, the result is the well-known allpass filter.
With some juggling, and letting
output, the result is the well-known allpass filter.
With some juggling, and letting
![]() , we arrive at the network
shown in part (b) of the figure. Allpass filters have many applications, some
of which we will visit later in this book.
, we arrive at the network
shown in part (b) of the figure. Allpass filters have many applications, some
of which we will visit later in this book.