Recirculating delay networks

It is sometimes desirable to connect the outputs of one or more delays in a network back into their own or each others' inputs. Instead of getting one or several echos of the original sound as in the simple example above, we can potentially get an infinite number of echos, each one feeding back into the network to engender yet others.

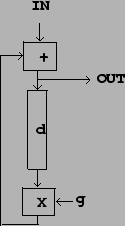
The simplest example of a recirculating network is the recirculating comb filter whose block diagram is shown in Figure 7.7. As with the earlier, simple comb filter, the input signal is sent down a delay line whose length is $d$ samples. Unlike the simple comb filter, the delay line's output is also inserted back in its input; the delay's input is now the sum of the original input and the delay output. The output is multiplied by a number $g$ before feeding it back into its input.

Figure 7.7: Block diagram for a recirculating comb filter. Here $d$ is the delay time in samples and $g$ is the feedback coefficient.

The time domain behavior of the recirculating comb filter is shown in Figure 7.8. Here we consider the effect of sending an impulse into the network. We get back the original impulse, plus a series of echos, each in turn $d$ samples after the previous one, and multiplied each time by the gain $g$. In general, a delay network's output given an impulse as input is called the network's impulse response.

Figure 7.8: Time-domain analysis of the recirculating comb filter, using an impulse as input.

Note that we have chosen a gain $g$ that is less than one in absolute value. If we chose a gain greater than one (or less than -1), each echo would have a larger magnitude than the previous one. Instead of falling exponentially as they do in the figure, they would grow exponentially. A recirculating network whose output eventually falls toward zero after its input terminates is called stable; one whose output grows without bound is called unstable.

We can also analyse the recirculating comb filter in the frequency domain. The situation is now complicated enough that it is almost prohibitively hard to analyze using real sinusoids, and so we get the first real payoff for having introduced complex numbers, which greatly simplify the analysis.

If, as before, we feed the input with the signal,

$$X[n] = Z^n$$

with $\vert Z\vert=1$, we can write the output as

$$Y[n] = (1 + g{Z^{-d}} + {g^2}{Z^{-2d}} + \cdots) X[n]$$

Here the terms in the sum come from the series of discrete echos. It follows that the amplitude of the output is:

$$H = 1 + g{Z^{-d}} + {(g{Z^{-d}})} ^ 2 + \cdots$$

This is a geometric series; we can sum it using the standard technique: first multiply both sides by $g{Z^{-d}}$ to give:

$$g{Z^{-d}} H = g{Z^{-d}} + {(g{Z^{-d}})} ^ 2 + {(g{Z^{-d}})} ^ 3 + \cdots$$

and subtract from the original equation to give:

$$H - g{Z^{-d}} H = 1,$$

and, solving for $H$,

$$H = {1 \over {1 - g{Z^{-d}}}}$$

A faster (but slightly less intuitive) method to get the same result is to examine the recirculating network itself to yield an equation for $H$, as follows. Since we named the input $X[n]$ and the output $Y[n]$, the signal going into the delay line is $X[n]+Y[n]$, and passing this through the delay line and multiplier gives

$$(X[n]+Y[n])g{Z^{-d}}$$

This is just the output signal again, so:

$$Y[n] = (X[n]+Y[n])g{Z^{-d}}$$

and dividing by $X[n]$ and using $H=Y[n]/X[n]$ gives:

$$H = (1 + H)g{Z^{-d}}$$

This is equivalent to the earlier equation for $H$.

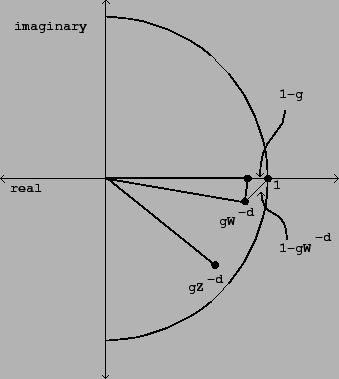
Now we would like to make a graph of the frequency response (the gain as a function of frequency) as we did for non-recirculating comb filters in Figure 7.6. This again requires that we make a preliminary picture in the complex plane. We would like to estimate the magnitude of $H$ equal to:

$$\vert H\vert = {1 \over {\vert 1 - g{Z^{-d}}\vert}}$$

where we used the multiplicative property of magnitudes to conclude that the magnitude of a (complex) reciprocal is the reciprocal of a (real) magnitude. Figure 7.9 shows the situation graphically. The gain $\vert H\vert$ is the reciprocal of the length of the segment reaching from the point 1 to the point $g{Z^{-d}}$. Figure 7.10 shows a graph of the frequency response $\vert H\vert$ as a function of the angular frequency $\omega = \angle(Z)$.

Figure 7.9: Diagram in the complex plane for approximating the output gain $\vert H\vert$ of the recirculating comb filters at three different frequencies: 0, and the arguments of two unit complex numbers $W$ and $Z$; $W$ is chosen to give a gain about 3 dB below the peak.

Figure 7.10: Frequency response of the recirculating comb filter with $g = 0.8$. The peak gain is $1/(1-g)$ = 5. Peaks are much narrower than for the simple comb filter.

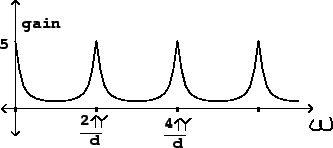Figure 7.9 can be used to analyze how the frequency response $\vert H(\omega)\vert$ should behave qualitatively as a function of $g$. The height and bandwidth of the peaks both depend on $g$. The maximum value that $\vert H\vert$ can attain is when

$${Z^{-d}} = 1$$

This occurs at the frequencies $\omega = 2\pi/d , 4\pi/d , \ldots$ as in the simple comb filter above. At these maxima it reaches

$$\vert H\vert = {1 \over {1 - g}}$$

The next important question is the bandwidth of the peaks in the frequency response. So we would like to find a particular frequency, $\angle(W)$, giving rise to a value of $\vert H\vert$ that is, say, 3 decibels below the maximum. To do this, we return to Figure 7.9, and try to find $W$ so that the distance from the point 1 to the point

$$1 - {W^{-d}}$$

is about $\sqrt{2}$ times the distance from 1 to $g$ (since $\sqrt{2}$:1 is a ratio of approximately 3 decibels).

We do this by arranging for the imaginary part of $W^{-d}$ to be roughly $1-g$ or its negative, making a nearly isosocles right triangle between the points 1, $1-g$, and $W^{-d}$. (Here we're supposing that $g$ is at least 2/3 or so; otherwise this approximation isn't very good). The hypoteneuse of a right isococles triangle is always $\sqrt{2}$ times the leg, and so the gain drops by that factor compared to its maximum.

We now make another approximation, that the imaginary part of $W^{-d}$ is approximately the angle in radians it cuts from the real axis:

$$\pm(1-g) \approx \mathrm{im}({W^{-d}}) \approx \angle({W^{-d}})$$

So the region of each peak reaching within 3 decibels of the maximum value is about

$$(1-g)/d$$

(in radians) to either side of the peak. The bandwidth narrows (and the filter peaks become sharper) as $g$ approaches its maximum value of $1$. .

As with the non-recirculating comb filter of section 9.2.1, the teeth of the comb are closer together for larger valuse of the delay $d$. On the other hand, a delay of $d=1$ (the shortest possible) gets only one tooth (at zero frequency) below the Nyquist frequency $\pi$ (the next tooth, at $2\pi$, corresponds again to a frequency of zero by foldover).

So the recirculating comb filter with $d=1$ is just a low-pass filter. Delay networks with one-sample delays will be the basis for designing many other kinds of digital filters in chapter 8.