Patch H06.envelope.follower.pd shows a simple realization of the envelope folower described in
section ![]() ; it is self-explanatory. An interesting
application of envelope following is shown in Patch H07.measure.spectrum.pd (Figure
8.30, part (a). A famous bell sample is looped as a test sound.
Rather than get the overall mean square power of the bell, we would like to
estimate the frequency and power of each of its partials. To do this we sweep
a band-pass filter up and down in frequency, listening to the result and/or
watching the filter's output power using an envelope follower. (We use
two band-pass filters in series for better isolation of the partials; this
is not especially good filter design but will do in this context.) When the
filter is tuned to a partial the envelope follower reports its strength.
; it is self-explanatory. An interesting
application of envelope following is shown in Patch H07.measure.spectrum.pd (Figure
8.30, part (a). A famous bell sample is looped as a test sound.
Rather than get the overall mean square power of the bell, we would like to
estimate the frequency and power of each of its partials. To do this we sweep
a band-pass filter up and down in frequency, listening to the result and/or
watching the filter's output power using an envelope follower. (We use
two band-pass filters in series for better isolation of the partials; this
is not especially good filter design but will do in this context.) When the
filter is tuned to a partial the envelope follower reports its strength.
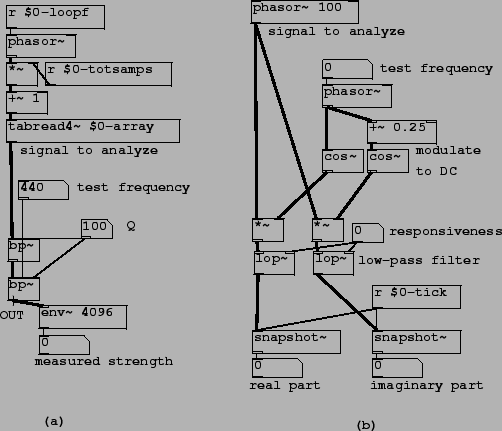 |
Patch H08.heterodyning.pd (part (b) of the figure) shows an alternative way of finding partial strengths of an incoming sound; it has the advantage of reporting the phase as well as the strength. First we modulate the desired partial down to zero frequency. We use a complex-valued sinusoid as a modulator so that we get only one sideband for each component of the input. The test frequency is the only frequency that is modulated to DC; others go elsewhere. We then low-pass the resulting complex signal. (We can use a real-valued low-pass filter separately on the real and imaginary parts.) This essentially removes all the partials except for the DC one, which we then harvest. This technique will be the basis of Fourier analysis, the subject of chapter 9.