




Next: Periodicity of the Fourier
Up: Fourier analysis of periodic
Previous: Fourier analysis of periodic
Contents
Index
Fourier transform as additive synthesis
Now consider an arbitrary signal ![$X[n]$](img705.png) that repeats every
that repeats every 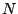 samples. (Previously we
had assumed that
samples. (Previously we
had assumed that ![$X[n]$](img705.png) could be obtained as a sum of sinusoids, but we haven't
yet found out whether any periodic
could be obtained as a sum of sinusoids, but we haven't
yet found out whether any periodic ![$X[n]$](img705.png) can be obtained that way.) Let
can be obtained that way.) Let
be the Fourier transform for
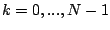 . Looking hard at
. Looking hard at ![$Y[k]$](img1104.png) we
see that it is a sum of complex sinusoids, with complex amplitudes
we
see that it is a sum of complex sinusoids, with complex amplitudes
![$X[n]$](img705.png) and frequencies
and frequencies 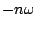 for
for
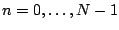 . In other words,
. In other words,
![$Y[k]$](img1104.png) can be considered as a waveform in its own right, whose
can be considered as a waveform in its own right, whose 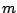 th component
has strength
th component
has strength ![$X[-m]$](img1106.png) . We can also find the amplitude of the partials of
. We can also find the amplitude of the partials of ![$Y[k]$](img1104.png) using the Fourier transform on
using the Fourier transform on ![$Y[k]$](img1104.png) . Equating the two expressions for the
partial amplitudes gives:
. Equating the two expressions for the
partial amplitudes gives:
(The expression ![$X[-m]$](img1106.png) makes sense because
makes sense because 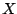 is a periodic signal). This
means in turn that
is a periodic signal). This
means in turn that ![$X[-m]$](img1106.png) can be obtained by summing sinusoids with
amplitudes
can be obtained by summing sinusoids with
amplitudes ![$Y[-k]/N$](img1108.png) . The same analysis starting with
. The same analysis starting with ![$X[-m]$](img1106.png) shows that
shows that
![$X[m]$](img1109.png) is obtained by summing sinusoids using
is obtained by summing sinusoids using ![$Y[k]/N$](img1110.png) as their amplitudes.
So now we know that any periodic
as their amplitudes.
So now we know that any periodic ![$X[n]$](img705.png) can indeed be obtained as a sum of
sinusoids. Furthermore, we know how to reconstruct a signal from its Fourier
transform, if we know its value for the integers
can indeed be obtained as a sum of
sinusoids. Furthermore, we know how to reconstruct a signal from its Fourier
transform, if we know its value for the integers
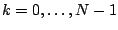 .
.





Next: Periodicity of the Fourier
Up: Fourier analysis of periodic
Previous: Fourier analysis of periodic
Contents
Index
Miller Puckette
2005-04-01
![]() that repeats every
that repeats every ![]() samples. (Previously we
had assumed that
samples. (Previously we
had assumed that ![]() could be obtained as a sum of sinusoids, but we haven't
yet found out whether any periodic
could be obtained as a sum of sinusoids, but we haven't
yet found out whether any periodic ![]() can be obtained that way.) Let
can be obtained that way.) Let