




Next: Properties of Fourier transforms
Up: Fourier analysis of periodic
Previous: Fourier transform as additive
Contents
Index
If X[n] is, as above, a signal that repeats every 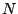 samples, the Fourier
transform of X[n] also repeats itself every
samples, the Fourier
transform of X[n] also repeats itself every 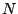 units of frequency, that is,
units of frequency, that is,
for all real values of 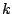 . This follows immediately from the definition
of the Fourier transform, since the factor
. This follows immediately from the definition
of the Fourier transform, since the factor
is unchanged when we add 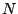 (or any multiple of
(or any multiple of 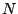 ) to
) to 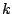 .
.
Miller Puckette
2005-04-01
![]() samples, the Fourier
transform of X[n] also repeats itself every
samples, the Fourier
transform of X[n] also repeats itself every ![]() units of frequency, that is,
units of frequency, that is,