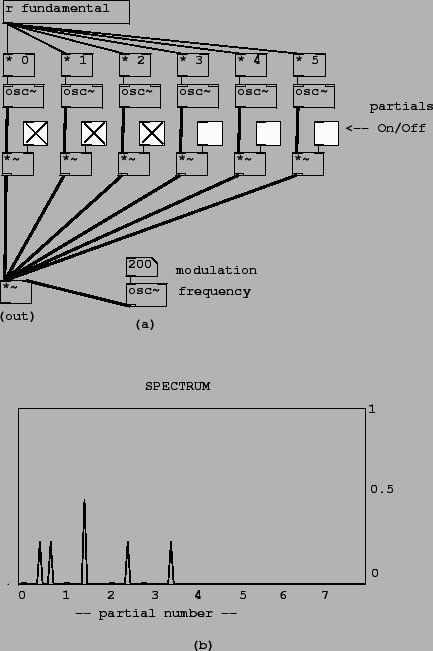
 |
The first Pd example for this chapter, E01.spectrum.pd, serves to introduce a spectrum measurement tool we'll use often. Here we will skip that and start with the second example, E02.ring.modulation.pd, which shows the effect of ring modulating a harmonic spectrum (which was worked out theoretically in section 5.2 and shown in Figure 5.4). In the example we consider a signal whose harmonics (from 0 through 5) all have unit amplitude. The partials may be turned on and off separately using toggle switches. When they are all on, the spectral envelope peaks at DC (because the constant signal is twice as strong as the other sinusoids), has a flat region from harmonics 1 through 5, and then descends to zero.
 |
In the signal generation portion of the patch (part (a) of the figure), we sum the six partials and multiply the sum by the single, modulating oscillator. (The six signals are summed implicitly by connecting them all to the same inlet of the *~ object.) The value of ``fundamental" at the top is computed to line up well with the spectral analysis, whose result is shown in part (b) of the figure.
The spectral analysis is done using techniques which won't be described until
chapter 9, but in sum, the output shows the location of the
sinusoids (assuming a discrete spectrum) on the horizontal axis and their
magnitudes on the vertical one. So the presence of a peak at DC of magnitude
one in the spectrum of the input signal predicts, ala figure 5.3,
that there should be a peak in the output spectrum, at the modulating frequency,
of height 1/2. Similarly, the two other sinusoids in the input signal, which
have height 1/2 in the spectrum, give rise to two peaks each, of height 1/4,
in the output. One of these four has been reflected about the left edge of
the figure (the ![]() axis.)
axis.)