Order of execution and lower limits on delay times

When using delays (as well as other state-sharing tilde objects in Pd), the order in which the delwrite~ and delread~ operations are done can affect the outcome of the computation. Although the tilde objects in a patch may have a complicated topology of audio connections, in reality Pd executes them all in a sequential order, one after the other, to compute each block of audio output. This linear order is guaranteed to be compatible with the audio interconnections, in the sense that no tilde object's computation is done until all its inputs, for that same block, have been computed.

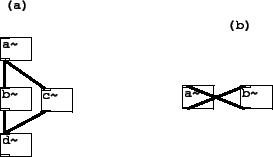
Figure 7.26 shows two examples of tilde object topologies and their translation into a sequence of computation. In part (a) there are four tilde objects, and because of the connections, the object a  must produce its output before either of b  or c  can run; and both of those in turn are used in the computation of d . So the possible orderings of these four objects are a-b-c-d and a-c-b-d. These two orderings will have exactly the same result unless the computation of b  and c  somehow affect each other's output (as delays might).

Figure 7.26: Order of execution of tilde objects in Pd: (a), an acyclic network. The objects may be executed in either the order a-b-c-d or a-c-b-d. In part (b), there is a cycle, and there is thus no compatible linear ordering of the objects because each one would need to be run before the other.

Part (b) of the figure shows a cycle of tilde objects. This network cannot be sorted into a compatible sequential order, since each of a  and b  requires the other's output to be computed first. In general, a sequential ordering of the tilde objects is possible if and only if there are no cycles anywhere in the network of tilde objects and their audio signal interconnections. Pd reports an error when such a cycle appears. (Note that the situation for control interconnections between objects is more complicated and flexible; see the Pd documentation for details.)

To see the effect of the order of computation on a delwrite~/delread~ pair, we can write explicitly the input and output signals in the two possible orders, with the minimum possible delay. If the write operation comes first, at a block starting at sample number $n$, the operation can be written as:

$$x[n], \ldots, x[n+B-1] \longrightarrow \fbox{\texttt{delwrite\~}}$$

where $B$ is the block size (as in Chapter 3). Having put those particular samples into the delay line, a following delread~ is able to read the same values out:

$$\fbox{\texttt{delread\~}} \longrightarrow x[n], \ldots, x[n+B-1]$$

On the other hand, suppose the delread~ object comes before the delwrite~. Then the samples $x[n], \ldots, x[n+B-1]$ have not yet been stored in the delay line, so the most recent samples that may be read belong to the previous block:

$$\fbox{\texttt{delread\~}} \longrightarrow x[n-B], \ldots, x[n-1]$$

$$x[n], \ldots, x[n+B-1] \longrightarrow \fbox{\texttt{delwrite\~}}$$

Here the minimum delay we can possibly obtain is the block size $B$. So the minimum delay is either $0$ or $B$, depending on the order in which the delread~ and delwrite~objects are sorted into a sequence of execution.

Looking back at the patches of Figures 7.24 and 7.25, which both feature recirculating delays, the delread~ object must be placed earlier in the sequence than the delwrite~ object. This is true of any design in which a delay's output is fed back into its input. The minimum possible delay is $B$ samples. For a (typical) sample rate of 44100 Hz. and block size of 64 samples, this comes to 1.45 milliseconds. This might not sound at first like a very important restriction. But if you are trying to tune a recirculating comb filter to a specific pitch, the highest you can get only comes to about 690 Hz. To get shorter recirculating delays you must increase the sample rate or decrease the block size.

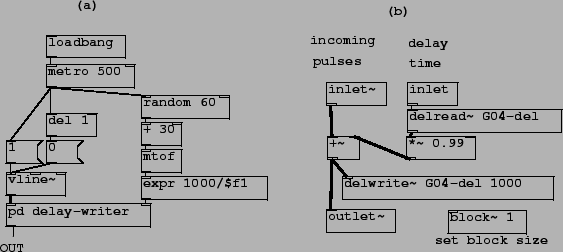
Patch G04.control.blocksize.pd (Figure 7.27) shows how the block size can be controlled in Pd using a new object:

Figure 7.27: A patch using block size control to lower the loop delay below the normal 64 samples: (a). the main patch; (b). the ``delay-writer" subpatch with a block~ object and a recirculating delay network.

,
: Set the local block size of the patch window the object sits in. Block sizes must be powers of two. The switch~ object, in addition, can be used to turn audio computation within the window on and off, using control messages. Additional creation arguments can set the local sample rate and specify overlapping computations (demonstrated in Chapter 9).

In part (a) of the figure (the main patch), a rectangular pulse is sent to the pd delay-writer subpatch, whose output is then returned to the main patch. Part (b) of the figure shows the contents of the subpatch, which sends the pulses into a recirculating delay. The block~ object specifies that, in this subpatch, signal computation uses a block size ($B$) of only one. So the minimum achievable delay is one sample instead of the default 64.

Putting a pulse (or other excitation signal) into a recirculating comb filter to make a pitch is sometimes called Karplus-Strong synthesis, having been described in a paper by them [KS83], although the idea seems to be older. It made its way for example into Paul Lansky's 1979 piece, Six Fantasies on a poem by Thomas Campion.