




Next: Elementary recirculating filter
Up: Designing filters
Previous: Elementary non-recirculating filter
Contents
Index
Non-recirculating filter, second form
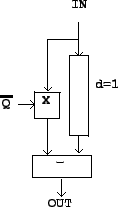
Occasionally we will use a variant of the filter above, as shown in Figure
8.10, called the elementary non-recirculating filter, second form.
Instead of multiplying the delay output by 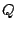 we multiply the direct signal
by its
complex conjugate
we multiply the direct signal
by its
complex conjugate
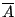 . (If
. (If
is any complex number, its complex conjugate is defined as:
Graphically this flips the entire complex plane across the real axis.)
The transfer function of the new filter is
This gives rise to the same frequency response as the first form since
Here we use the fact that
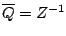 , for all unit complex
numbers
, for all unit complex
numbers
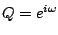 , since
, since
Although the two forms of the elementary non-recirculating filter have the same
frequency response, their phase responses are different, and we will
occasionally use the second form for its phase response.
Figure 8.10:
The elementary non-recirculating filter, second form.
 |





Next: Elementary recirculating filter
Up: Designing filters
Previous: Elementary non-recirculating filter
Contents
Index
Miller Puckette
2006-03-03
![]() we multiply the direct signal
by its
complex conjugate
we multiply the direct signal
by its
complex conjugate
![]() . (If
. (If