




Next: Time-varying coefficients
Up: Designing filters
Previous: Stretching the unit circle
Contents
Index
We can apply the above to transform the Butterworth filter into a high-quality
band-pass filter with center frequency 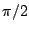 . A further transformation
can then be applied to shift the center frequency to any desired value
. A further transformation
can then be applied to shift the center frequency to any desired value 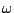 between 0 and
between 0 and 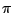 . The transformation will be of the form,
. The transformation will be of the form,
where 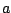 and
and 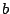 are real numbers and not both are zero. This
is a particular case of the general form given above for unit-circle-preserving
rational functions. We can check moreover that
are real numbers and not both are zero. This
is a particular case of the general form given above for unit-circle-preserving
rational functions. We can check moreover that 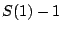 and
and 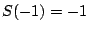 ,
and that the top and bottom halves of the unit circle are transformed
symmetrically; if
,
and that the top and bottom halves of the unit circle are transformed
symmetrically; if 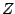 goes to
goes to 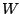 then
then 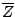 goes to
goes to 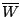 .
The qualitative effect of the transformation
.
The qualitative effect of the transformation 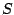 is to slide points of the
unit circle, non-uniformly, toward
is to slide points of the
unit circle, non-uniformly, toward 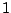 or
or 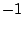 .
.
In particular, we wish to choose 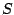 so that:
so that:
If we do that, keep 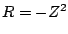 as before, and let
as before, and let 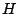 be the transfer
function for a low-pass Butterworth filter, then the combined filter
with transfer function
be the transfer
function for a low-pass Butterworth filter, then the combined filter
with transfer function 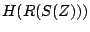 will be a band-pass filter with center frequency
will be a band-pass filter with center frequency 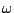 . Solving for
. Solving for 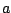 and
and 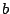 gives:
gives:
The new transfer function, 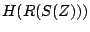 , will have
, will have 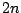 poles and
poles and 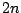 zeros (if
zeros (if 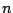 is the degree of the Butterworth filter
is the degree of the Butterworth filter 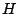 ).
).
Knowing the transfer function is good, but even better is knowing the locations
of all the poles and zeros of the new filter, which we need to be able to
compute it using elementary filters. If 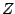 is a pole of the transfer
function
is a pole of the transfer
function
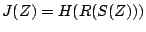 , that is, if
, that is, if 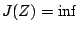 , then
, then 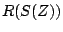 must
be a pole of
must
be a pole of 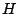 . The same goes for zeros. To find a pole or zero of
. The same goes for zeros. To find a pole or zero of 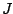 we set
we set 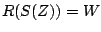 , where
, where 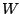 is a pole or zero of
is a pole or zero of 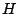 , and solve for
, and solve for 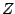 .
This gives:
.
This gives:
(Here 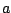 and
and 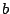 are as given above and we have used the fact that
are as given above and we have used the fact that
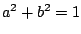 ). A sample pole-zero plot and frequency response of
). A sample pole-zero plot and frequency response of  are shown in Figure 8.20.
are shown in Figure 8.20.
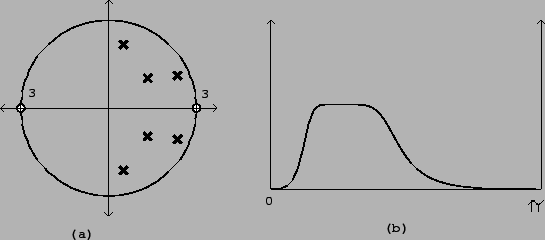
Figure 8.20:
Butterworth band-pass filter: (a) pole-zero diagram; (b)
frequency response. The center frequency is 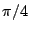 . The bandwidth depends
both on center frequency and on the bandwidth of the original Butterworth
low-pass filter used.
. The bandwidth depends
both on center frequency and on the bandwidth of the original Butterworth
low-pass filter used.
 |





Next: Time-varying coefficients
Up: Designing filters
Previous: Stretching the unit circle
Contents
Index
Miller Puckette
2006-03-03
![]() . A further transformation
can then be applied to shift the center frequency to any desired value
. A further transformation
can then be applied to shift the center frequency to any desired value ![]() between 0 and
between 0 and ![]() . The transformation will be of the form,
. The transformation will be of the form,
![]() so that:
so that:
![]() is a pole of the transfer
function
is a pole of the transfer
function
![]() , that is, if
, that is, if ![]() , then
, then ![]() must
be a pole of
must
be a pole of ![]() . The same goes for zeros. To find a pole or zero of
. The same goes for zeros. To find a pole or zero of ![]() we set
we set ![]() , where
, where ![]() is a pole or zero of
is a pole or zero of ![]() , and solve for
, and solve for ![]() .
This gives:
.
This gives:
