 |
 |
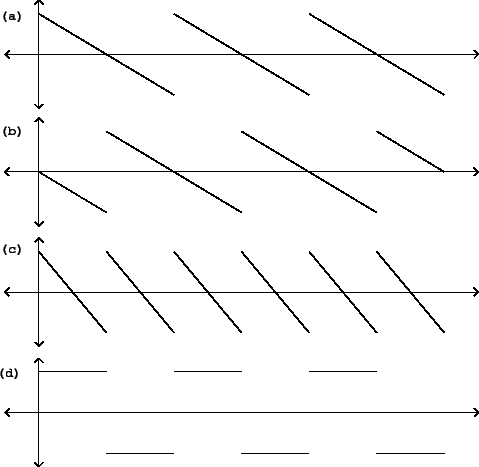
As an example, we apply the shift symmetry (even and odd harmonics) to a sawtooth wave. Figure 10.2 (part a) shows the original sawtooth wave and part b shows the result of shifting by a half cycle. The sum of the two (part c) drops discontinuously whenever either one of the two copies does so, and traces a line segment whenever both component sawtooth waves do; so it in turn becomes a sawtooth wave, of half the original period (twice the fundamental frequency). The difference of the two sawtooth waves has slope zero except for the discontinuities. The discontinuities coming from the original sawtooth wave jump in the same direction (negative to positive), but those coming from the shifted one are negated and jump from positive to negative. The result is a square wave, a special case of the rectangle wave where the two component segments have the same duration.
This symmetry was used to great effect in the design of Buchla analog synthesizers in the 1970s; instead of offering a single sawtooth generator, Buchla designed an oscillator which outputs the even and odd harmonic portions separately, so that cross-fading between the two allows a continuous control over the relative strengths of the even and odd harmonics in the analog waveform.