Among the several conclusions we can draw from the even/odd harmonic decomposition of the sawtooth wave (Figure 10.2), one is that a square wave can be decomposed into a linear combination of two sawtooth waves. We can carry this idea further, and show how to compose any classical waveform having only jumps (discontinuities in value) but no corners (discontinuities in slope) as a sum of sawtooth waves of various phases and amplitudes. We then develop the idea further, showing how to generate waveforms with corners (either in addition to, or instead of, jumps) using another fundamental waveform we'll call the parabolic wave.
Suppose first that a waveform of period ![]() has discontinuities at
has discontinuities at ![]() different points,
different points,
![]() , all lying on the cycle between 0 and
, all lying on the cycle between 0 and
![]() , at which the waveform jumps by values
, at which the waveform jumps by values
![]() . A negative
value of
. A negative
value of ![]() , for instance, would mean that the waveform jumps from a higher
to a lower value at the point
, for instance, would mean that the waveform jumps from a higher
to a lower value at the point ![]() , and a positive value of
, and a positive value of ![]() would mean
a jump from a lower to a higher value.
would mean
a jump from a lower to a higher value.
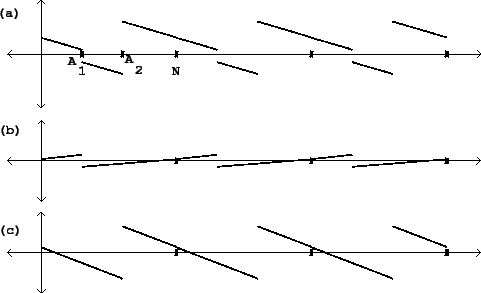 |
For instance, Figure 10.3 shows (part a) a classical waveform with
two jumps:
![]() and
and
![]() .
Parts (b) and (c) show sawtooth waves which each has one of the two jumps. The
sum of the two sawtooth waves reconstructs the waveform of part (a), except for
a possible constant (DC) offset.
.
Parts (b) and (c) show sawtooth waves which each has one of the two jumps. The
sum of the two sawtooth waves reconstructs the waveform of part (a), except for
a possible constant (DC) offset.
The sawtooth wave with a jump of one unit at the point zero is given by
The slopes of the segments of the classical waveform of part (a) are all equal,
and equal the sum of the slopes of the component sawtooth waves, equal in
general to
To decompose classical waveforms with corners we use the parabolic wave, which,
over a single period from 0 to ![]() , is equal to
, is equal to
To construct a waveform with any desired number of corners (suppose they are
at the points
![]() , at which we want the slope changes to
equal
, at which we want the slope changes to
equal
![]() ), we sum up the necessary parabolic waves:
), we sum up the necessary parabolic waves:
If the sum ![]() is to contain line segments (not segments of curves), the
is to contain line segments (not segments of curves), the
![]() terms in the sum must sum to zero. From the expansion of
terms in the sum must sum to zero. From the expansion of ![]() above,
this implies that
above,
this implies that
![]() . Analyses of complex
waveforms (as in the figure) will always satisfy this condition because the
changes in slope, over a cycle, must all add to zero for the waveform to
connect with itself.
. Analyses of complex
waveforms (as in the figure) will always satisfy this condition because the
changes in slope, over a cycle, must all add to zero for the waveform to
connect with itself.