We have been routinely adding audio signals together, and multiplying them by slowly-varying signals (used as amplitude envelopes for example) since chapter 1. In order to complete our understanding of the algebra of audio signals we now consider the situation where we multiply two audio signals neither of which may be assumed to change slowly. The key to understanding what happens is the:
We can use this formula to see what happens when we multiply two SINUSOIDS
(page ![]() ):
):
This gives us a very easy to use tool for shifting the component frequencies of a sound, called ring modulation, which is shown in its simplest form in Figure 5.2. An oscillator provides a carrier signal, which is simply multiplied by the input. In this context the input is called the modulating signal. The term ``ring modulation" is often used more generally to mean multiplying any two signals together, but here we'll just consider using a sinusoidal carrier signal.
Figure 5.3 shows a variety of results that may be obtained by
multiplying a (modulating) sinusoid of angular frequency ![]() and
RMS amplitude
and
RMS amplitude
![]() , by a (carrier) sinusoid of angular frequency
, by a (carrier) sinusoid of angular frequency ![]() and amplitude 1:
and amplitude 1:
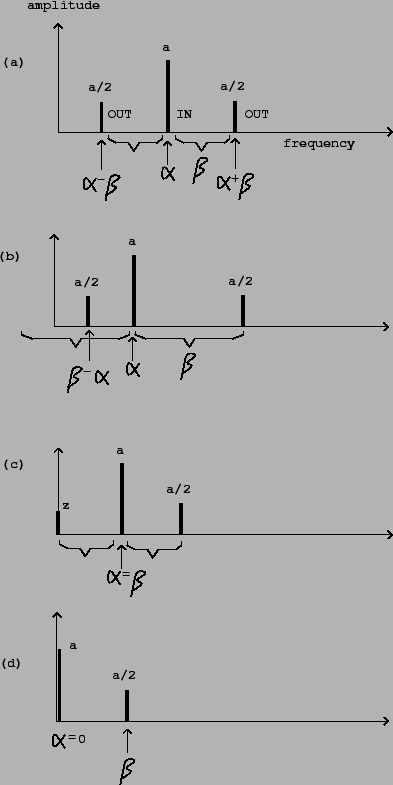 |
Parts (a) and (b) of the figure show ``general" cases where ![]() and
and ![]() are
nonzero and different from each other. The component frequencies of the output
are
are
nonzero and different from each other. The component frequencies of the output
are
![]() and
and
![]() . In part (b), since
. In part (b), since
![]() ,
we get a negative frequency component. Since cosine is an even function, we
have
,
we get a negative frequency component. Since cosine is an even function, we
have
In the special case where
![]() , the second (difference) sideband
has zero frequency. In this case phase will be significant so we rewrite
the product with explicit phases, replacing
, the second (difference) sideband
has zero frequency. In this case phase will be significant so we rewrite
the product with explicit phases, replacing ![]() by
by ![]() , to get:
, to get:
Finally, part (d) of the figure shows a carrier signal whose frequency is
zero. Its value is just the constant ![]() . In this case we get only one
sideband, of amplitude
. In this case we get only one
sideband, of amplitude ![]() as usual.
as usual.
We can use the distributive rule for multiplication to find out what
happens when we multiply signals together which consist of more than one
partial each. For example, in the situation above we can replace the
signal of frequency ![]() with a sum of several sinusoids, such as:
with a sum of several sinusoids, such as:
Figure 5.4 shows the result of multiplying a complex periodic signal
(with several components tuned in the ratio 0:1:2:![]() ) by a
sinusoid. Both the spectral envelope and the component frequencies of the
result transform by relatively simple rules.
) by a
sinusoid. Both the spectral envelope and the component frequencies of the
result transform by relatively simple rules.
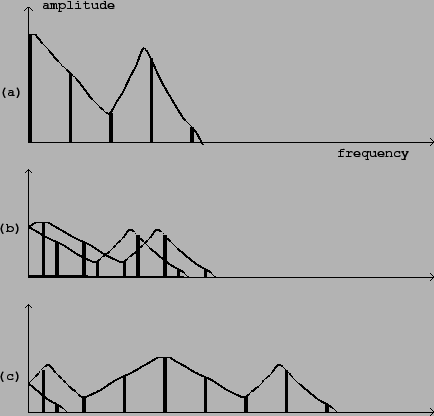 |
The resulting spectrum is essentially the original spectrum combined with its reflection about the vertical axis. This combined spectrum is then shifted to the right by the modulating frequency. Finally, if any components of the shifted spectrum are still left of the vertical axis, they are reflected about it to make positive frequencies again.
In part (b) of the figure, the modulating frequency (the frequency of the sinusoid) is below the fundamental frequency of the complex signal. In this case the shifting is by a relatively small distance, so that re-folding the spectrum at the end almost places the two halves on top of each other. The result is a spectral envelope roughly the same as the original (although half as high) and a spectrum twice as dense.
A special case, not shown, is modulation by a frequency exactly half the
fundamental. In this case, pairs of partials will fall on top of each other,
and will have the ratios 1/2 : 3/2 : 5/2 :![]() - an odd-partial-only signal
an octave below the original. This is a very simple and effective octave divider
for a harmonic signal, asuming you know or can find its fundamental frequency.
If you want even partials as well as odd ones (for the octave-down signal),
simply mix the original signal with the modulated one.
- an odd-partial-only signal
an octave below the original. This is a very simple and effective octave divider
for a harmonic signal, asuming you know or can find its fundamental frequency.
If you want even partials as well as odd ones (for the octave-down signal),
simply mix the original signal with the modulated one.
Part (c) of the figure shows the effect of using a modulating frequency much higher than the fundamental frequency of the complex signal. Here the unfolding effect is much more clearly visible (only one partial, the leftmost one, had to be reflected to make its frequency positive.) The spectral envelope is now widely displaced from the original; this displacement is often a more strongly audible effect than the relocation of partials.
In another special case, the modulating frequency may be a multiple of the fundamental of the complex periodic signal; in this case the partials all land back on other partials of the same fundamental, and the only effect is the shift in spectral envelope.