General (non-symmetric) triangle wave

Figure 10.7: Non-symmetric triangle wave, with vertices at $(M, 1)$ and $(N-M, -1)$.

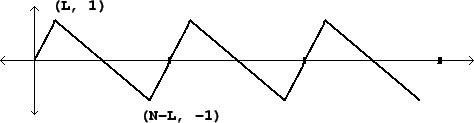
A general, non-symmetric triangle wave appears in Figure 10.7. Here we have arranged the cycle so that, first, the DC component is zero (so that the two corners have equal and opposite heights), and second, so that the midpoint of the shorter segment goes through the point $(0,0)$.

The two line segments have slopes equal to $1/M$ and $-2/(N-2M)$, so the decomposition into component parabolic waves is given by:

$$x[n] = {{N^2} \over {MN - 2{M^2}}} (p[n+M] - p[n-M])$$

(here we're using the periodicity of $p[n]$ to replace $p[n-(N-M)]$ by $p[n+M]$).)

The most general way of dealing with linear combinations of elementary (parabolic and/or sawtooth) waves is to go back to the complex Fourier series, as we did in finding the series for the elementary waves themselves. But in this particular case we can use a trigonometric identity to avoid the extra work of converting back and forth. Just plug in the real-valued Fourier series:

$$x[n] = {{N^2} \over {2{\pi ^ 2} (MN - 2{M^2})}} \left [ {\cos ( \omega (n-M))} - {\cos ( \omega (n+M))} \right .$$

$$\left . + {{\cos ( 2 \omega (n-M)) - \cos ( 2 \omega (n+M))} \over 4} + \cdots \right ]$$

Now we use the identity,

$$\cos(a) - \cos(b) = 2 \sin({{b-a}\over 2}) \sin({{a+b}\over 2})$$

so that, for example,

$${\cos ( \omega (n-M))} - {\cos ( \omega (n+M))} = 2 \sin (2 \pi M / N) \sin ( \omega n)$$

(Here again we used the definition of $\omega=2\pi/N$.) This is a simplification since the first sine term does not depend on $n$, and hence is just an amplitude term. Applying the identity to all the terms of the expansion for $x[n]$ gives:

$$x[n] = a[1] \sin(\omega n) + a[2] \sin(2 \omega n) + \cdots$$

where the amplitudes of the components are given by:

$$a[k] = {1 \over {{\pi ^ 2} (M/N - 2{{(M/N)}^2})}} \cdot {{\sin (2 \pi k M / N) } \over {k^2}}$$

Notice that the result does not depend separately on the values of $M$ and $N$, but only on their ratio, $M/N$ (this is not surprising because the shape of the waveform depends on this ratio). If we look at small values of $k$:

$$k < {{1} \over {4 M/N}}$$

the argument of the sine function is less than $\pi /2$ and using the approximation $\sin(\theta) \approx \theta$ we find that $a[k]$ drops off as $1/k$, just as the partials of a sawtooth wave. But for larger values of $k$ the sine term oscillates between 1 and -1, so that the amplitudes drop off irregularly as $1/{k^2}$.

Figure 10.8 shows the partial strengths with $M/N$ set to 0.03; here, our prediction is that the $1/k$ dependence should extend to $k \approx 1/(4\cdot 0.03) \approx 8.5$, in rough agreement with the figure.

Another way to see why the partials should behave as $1/k$ for low values of $k$ and $1/{k^2}$ thereafter, is to compare the period of a given partial with the length of the short segment, $2M$. For partials numbering less than $N/4M$, the period is at least twice the length of the short segment, and at that scale the waveform is nearly indistinguishable from a sawtooth wave. For partials numbering in excess of $N/2M$, the two corners of the triangle wave are at least one period apart, and at these higher frequencies the two corners (each with $1/{k^2}$ frequency dependence) are resolved from each other. In the figure, the notch at partial 17 occurs at the wavelength $N/2M \approx 1/17$, at which wavelength the two corners are one cycle apart; since the corners are opposite in sign they cancel each other.