Variable and fractional shifts

Like any audio synthesis or processing technique, delay networks become much more powerful and interesting if their characteristics can be made to change over time. The gain parameters (such as $g$ in the recirculating comb filter) may be controlled by envelope generators, varying them while avoiding clicks or other artifacts. The delay times (such as $d$ before) are not so easy to vary smoothly for two reasons.

First, we have only defined time shifts for integer values of $d$, since for fractional values of $d$ an expression such as $x[n-d]$ is not determined if $x[n]$ is only defined for integer values of $n$. To make fractional delays we will have to introduce some suitable interpolation scheme. And if we wish to vary $d$ smoothly over time, it will not give good results simply to hop from one integer to the next.

Second, even once we have achieved perfectly smoothly changing delay times, the artifacts caused by varying delay time become noticeable even at very small relative rates of change; while in most cases you may ramp an amplitude control between any two values over 30 milliseconds without trouble, changing a delay by only one sample out of every hundred makes a very noticeable shift in pitch--indeed, one frequently will vary a delay deliberately in order to hear the artifacts, only incidentally passing from one specific delay time value to another one.

The first matter (fractional delays) can be dealt with using an interpolation scheme, in exactly the same way as for wavetable lookup (Section 2.5). For example, suppose we want a delay of $d=1.5$ samples. For each $n$ we must estimate a value for $x[n-1.5]$. We could do this using standard four-point interpolation, putting a cubic polynomial through the four ``known" points (0, x[n]), (1, x[n-1]), (2, x[n-2]), (3, x[n-3]), and then evaluating the polynomial at the point 1.5. Doing this repeatedly for each value of $n$ gives the delayed signal.

This four-point interpolation scheme can be used for any delay of at least one sample. Delays of less than one sample can't be calculated this way because we need two input points at least as recent as the desired delay. They were available in the above example, but for a delay time of 0.5 samples, for instance, we would need the value of $x[n+1]$, which is in the future.

The accuracy of the estimate could be further improved by using higher-order interpolation schemes. However, there is a trade-off between quality and computational efficiency. Furthermore, if we move to higher-order interpolation schemes, the minimum possible delay time will increase, causing trouble in some situations.

The second matter to consider is the artifacts--whether wanted or unwanted-- that arise from changing delay lines. In general, a discontinuous change in delay time will give rise to a discontinuous change in the output signal, since it is in effect interrupted at one point and made to jump to another. If the input is a sinusoid, the result is a discontinuous phase change.

If it is desired to change the delay line occasionally between fixed delay times (for instance, at the beginnings of musical notes), then we can use the techniques for managing sporadic discontinuities that were introduced in Section 4.3. In effect these techniques all work by muting the output in one way or another. On the other hand, if it is desired that the delay time change continuously--while we are listening to the output--then we must take into account the artifacts that result from the changes.

Figure 7.17: A variable length delay line, whose output is the input from some previous time. The output samples can't be newer than the input samples, nor older than the length $D$ of the delay line. The slope of the input/output curve controls the momentary transposition of the output.

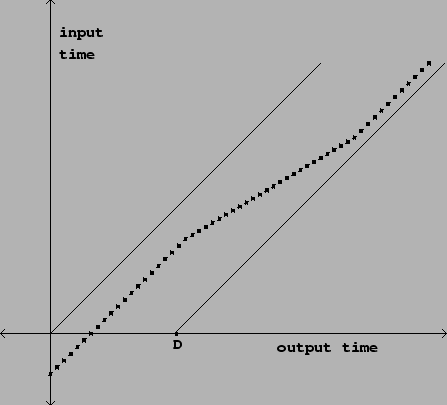Figure 7.17 shows the relationship between input and output time in a variable delay line. The delay line is assumed to have a fixed maximum length $D$. At each sample of output (corresponding to a point on the horizontal axis), we output one (possibly interpolated) sample of the delay line's input. The vertical axis shows which sample (integer or fractional) to use from the input signal. Letting $n$ denote the output sample number, the vertical axis shows the quantity $n - d[n]$, where $d[n]$ is the (time-varying) delay in samples. If we denote the input sample location by:

$$y[n] = n - d[n]$$

then the output of the delay line is:

$$z[n] = x[y[n]]$$

where the signal $x$ is evaluated at the point $y[n]$, interpolating appropriately in case $y[n]$ is not an integer. This is exactly the formula for wavetable lookup (Page ). We can use all the properties of wavetable lookup of recorded sounds to predict the behavior of variable delay lines.

There remains one difference between delay lines and wavetables: the material in the delay line is constantly being refreshed. Not only can we not read into the future, but, if the the delay line is $D$ samples in length, we can't read further than $D$ samples into the past either:

$$0 < d[n] < D$$

or, negating this and adding $n$ to each side,

$$n > y[n] > n - D.$$

This last relationship appears as the region between the two diagonal lines in Figure 7.17; the function $y[n]$ must stay within this strip.

Returning to Section 2.2, we can use the Momentary Transposition Formulas for Wavetables to calculate the transposition $t[n]$ of the output. This gives the Momentary Transposition Formula for delay lines:

$$t[n] = y[n] - y[n-1] = 1 - (d[n] - d[n-1])$$

If $d[n]$ does not change with $n$, the transposition factor is $1$ and the sound emerges from the delay line at the same speed as it went in. But if the delay time is increasing as a function of $n$, the resulting sound is transposed downward, and if $d[n]$ decreases, upward.

This is called the Doppler effect, and it occurs in nature as well. The air that sound travels through can sometimes be thought of as a delay line. Changing the length of the delay line corresponds to moving the listener toward or away from a stationary sound source; the Doppler effect from the changing path length works precisely the same in the delay line as it would be in the physical air.

Returning to Figure 7.17, we can predict that there is no pitch shift at the beginning, but then when the slope of the path decreases the pitch will drop for an interval of time before going back to the original pitch (when the slope returns to one). The delay time can be manipulated to give any desired transposition, but the greater the transposition, the less long we can maintain it before we run off the bottom or the top of the diagonal region.