Envelope following

It is frequently desirable to use the time-varying power of an incoming signal to trigger or control a musical process. To do this, we will need a procedure for measuring the power of an audio signal. Since most audio signals pass through zero many times per second, it won't suffice to take instantaneous values of the signal to measure its power; instead, we must calculate the average power over an interval of time long enough that its variations won't show up in the power estimate, but short enough that changes in signal level are quickly reflected in the power estimate. A computation that provides a time-varying power estimate of a signal is called an envelope follower.

The output of a low-pass filter can be viewed as a moving average of its input. For example, suppose we apply a normalized one-pole low-pass filter with coefficient $p$, as in Figure 8.21, to an incoming signal $x[n]$. The output (call it y[n]) is the sum of the delay output times $p$, with the input times $1-p$:

$$y[n] = p \cdot y[n-1] + (1-p) \cdot x[n]$$

so each input is averaged, with weight $1-p$, into the previous output to produce a new output. So we can make a moving average of the square of an audio signal using the diagram of Figure 8.26. The output is a time-varying average of the instantaneous power $x[n]^2$, and the design of the low-pass filter controls, among other things, the settling time of the moving average.

Figure 8.26: Envelope follower. The output is the average power of the input signal.

For more insight into the design of a suitable low-pass filter for an envelope follower, we analyze it from the point of view of signal spectra. If, for instance, we put in a real-valued sinusoid:

$$x[n] = a \cdot \cos(\alpha n)$$

the result of squaring is:

$${{x[n]}^2} = {{a^2}\over 2} \left ( \cos(2 \alpha n) + 1 \right )$$

and so if the low-pass filter effectively stops the component of frequency $2 \alpha$ we will get out approximately the constant ${{a^2} / 2}$, which is indeed the average power.

The situation for a signal with several components is similar. Suppose the input signal is now,

$$x[n] = a \cdot \cos(\alpha n) + b \cdot \cos(\beta n)$$

whose spectrum is plotted in Figure 8.27 (part a). (We have omitted the two phase terms but they will have no effect on the outcome.) Squaring the signal produces the spectrum shown in part (b) (see Section 5.2).) We can get the desired fixed value of $({a^2} + {b^2})/2$ simply by filtering out all the other components; ideally the result will be a constant (DC) signal. As long as we filter out all the partials, and also all the difference tones, we end up with a stable output that correctly estimates the average power.

Figure 8.27: Envelope following from the spectral point of view: (a) an incoming signal with two components; (b) the result of squaring it.

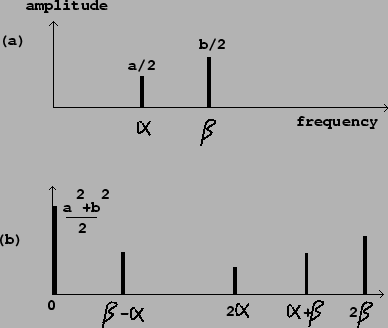Envelope followers may also be used on noisy signals, which may be thought of as signals with dense spectra. In this situation there will be difference frequencies arbitrarily close to zero, and filtering them out entirely will be impossible; we will always get fluctuations in the output, but they will decrease proportionally as the filter's passband is narrowed.

Although a narrower passband will always give a cleaner output, whether for discrete or continuous spectra, the filter's settling time will lengthen proportionally as the passband is narrowed. There is thus a tradeoff between getting a quick response and a smooth result.