Phase vocoder time bender

Figure 9.18: Phase vocoder for time stretching and contraction.

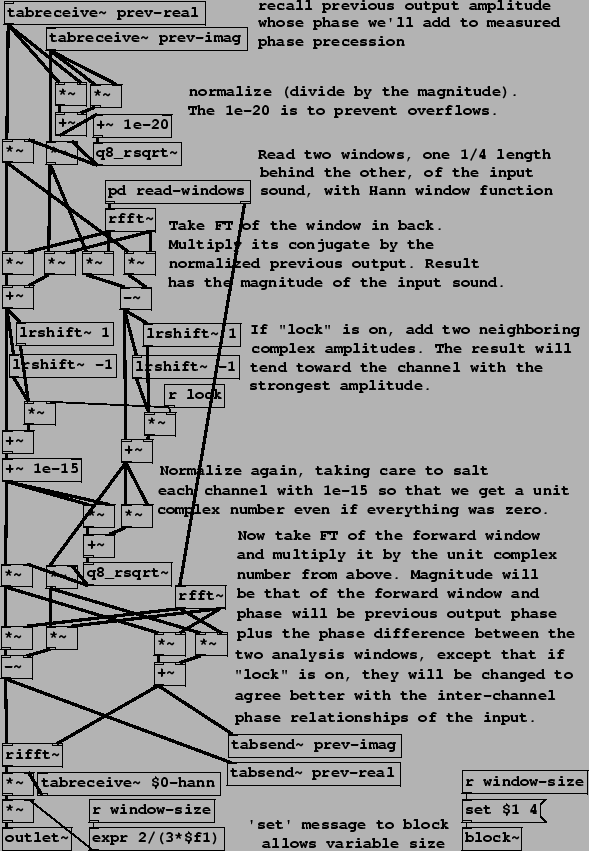
The phase vocoder usually refers to the general technique of passing from (complex-valued) channel amplitudes to pairs consisting of (real-valued) magnitudes and phase precession rates (``frequencies"), and back, as described in Figure 9.11 (Section 9.5). In Example I07.phase.vocoder.pd (Figure 9.18), we use this technique with the specific aim of time-stretching and/or time-contracting a recorded sound under real-time control. That is, we control, at any moment in real time, the location in the recorded sound we hear. Two new objects are used:

: shift a block left or right (according to its creation argument). If the argument is positive, each block of the output is the input shifted that number of spaces to the right, filling zeros in as needed on the left. A negative argument shifts to the left, filling zeros in at the right.

: quick and approximate reciprocal square root. Outputs the reciprocal of the square root of its input, good to about a part in 256, using much less computation than a full-precision square root and reciprocal would.

The process starts with a sub-patch, pd read-windows, that outputs two Hann-windowed blocks of the recorded sound, a ``back" one and a ``front" one 1/4 window further forward in the recording. The window shown uses the two outputs of the sub-patch to guide the amplitude and phase change of each channel of its own output.

The top two tabreceive~ objects recall the previous block of complex amplitudes sent to the rifft~ object at bottom, corresponding to $S[m-1,k]$ in the discussion of Section 9.5. The patch as a whole computes $S[m, k]$ and then its Hann windowed inverse FT for output.

After normalizing $S[m-1,k]$, its complex conjugate (the normalized inverse) is multiplied by the windowed Fourier transform of the ``back" window $T[k]$, giving the product $R[k]$ of Page . Next, depending on the value of the parameter ``lock", the computed value of $R[k]$ is conditionally replaced with the phase-locking version $R'[k]$. This is done using lrshift~ objects, whose outputs are added into $R[k]$ if ``lock" is set to one, or otherwise not if it is zero. The result is then normalized and multiplied by the Hann-windowed Fourier transform of the ``front" window ($T'[k]$) to give $S[m, k]$.

Three other applications of Fourier analysis/resynthesis, not pictured here, are provided in the Pd examples. First, Example I08.pvoc.reverb.pd shows how to make a phase vocoder whose output recirculates as in a reverberator, except that individual channels are replaced by the input when it is more powerful than what is already recirculating. The result is a more coherent-sounding reverberation effect than can be made in the classical way using delay lines.

Example I09.sheep.from.goats.pd demonstrates the (imperfect) technique of separating pitched signals from noisy ones, channel by channel, based on the phase coherence we should expect from a Hann-windowed sinusoid. If three adjacent channels are approximately $\pi$ radians out of phase from each other, they are judged to belong to a sinusoidal peak. Channels belonging to sinusoidal peaks are replaced with zero to extract the noisy portion of the signal, or all others are replaced with zero to give the sinusoidal portion.

Example I10.phase.bash.pd returns to the wavetable looping sampler of Figure 2.7, and shows how to align the phases of the sample so that all components of the signal have zero phase at points 0, $N$, $2N$, and so on. In this way, two copies of a looping sampler placed $N$ samples apart can be coherently cross-faded. A synthetic, pitched version of the original soundfile can be made using daisy-chained cross-fades.