




Next: Classical waveforms
Up: Fourier analysis and resynthesis
Previous: Phase vocoder time bender
Contents
Index
- A signal
![$x[n]$](img80.png) is 1 for
is 1 for 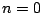 and
and 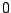 otherwise (an impulse). What is
its (
otherwise (an impulse). What is
its (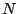 -point) Fourier transform as a function of
-point) Fourier transform as a function of 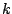 ?
?
- Assuming further that
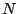 is an even number, what does
the Fourier transform become if
is an even number, what does
the Fourier transform become if ![$x[n]$](img80.png) is 1 at
is 1 at 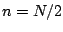 instead of at
instead of at 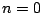 ?
?
- For what integer values of
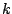 is the Fourier transform of the
is the Fourier transform of the 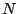 -point
Hann window function nonzero?
-point
Hann window function nonzero?
- In order to Fourier analyze a 100-Hertz periodic tone (at a sample rate
of 44100 Hertz), using a Hann window, what value of
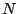 would be needed to
completely resolve all the partials of the tone (in the sense of having
non-overlapping peaks in the spectrum)?
would be needed to
completely resolve all the partials of the tone (in the sense of having
non-overlapping peaks in the spectrum)?
- Suppose an N-point Fourier transform is done on a complex sinusoid of frequency
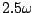 where
where 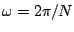 is the fundamental frequency. What percentage
of the signal energy lands in the main lobe, channels
is the fundamental frequency. What percentage
of the signal energy lands in the main lobe, channels 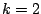 and
and 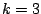 ? If the signal
is Hann windowed, what percentage of the energy is now in the main lobe (which
is then channels 1 through 4)?
? If the signal
is Hann windowed, what percentage of the energy is now in the main lobe (which
is then channels 1 through 4)?





Next: Classical waveforms
Up: Fourier analysis and resynthesis
Previous: Phase vocoder time bender
Contents
Index
Miller Puckette
2006-12-30