Another approach to modulating a signal, called
waveshaping,
is simply to pass it through a
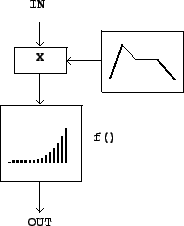
suitably chosen nonlinear function. A block diagram for doing this is shown in Figure
5.5.
The function ![]() (called the
transfer function)
distorts the incoming waveform into a different shape. The new shape depends
on the shape of the incoming wave, on the transfer function, and
also--importantly--on
the amplitude of the incoming signal. Since the amplitude of the input
waveform affects the shape of the output waveform (and hence the timbre),
this gives us an easy way to make a continuously varying family of timbres,
simply by varying the input level of the transformation. For this reason,
it is customary to include a leading amplitude control as part of the waveshaping
operation, as shown in the block diagram.
(called the
transfer function)
distorts the incoming waveform into a different shape. The new shape depends
on the shape of the incoming wave, on the transfer function, and
also--importantly--on
the amplitude of the incoming signal. Since the amplitude of the input
waveform affects the shape of the output waveform (and hence the timbre),
this gives us an easy way to make a continuously varying family of timbres,
simply by varying the input level of the transformation. For this reason,
it is customary to include a leading amplitude control as part of the waveshaping
operation, as shown in the block diagram.
 |
The amplitude of the sinusoid is called the waveshaping index. In many situations a small index leads to relatively little distortion (hence a more nearly sinusoidal output) and a larger one gives a more distorted, hence richer, timbre.
Figure 5.6 shows a familiar example of waveshaping, in which
![]() amounts to a
clipping function. This example shows clearly how the input
amplitude--the index--can
affect the output waveform. The clipping function passes its input
to the output unchanged as long as it stays in the interval between -0.3 and
+0.3. So when the input (in this case a sinusoid) does not exceed 0.3 in
absolute value, the output is the same as the input. But when the input grows
past the 0.3 limit, it is limited to 0.3; and as the amplitude of the
signal increases the effect of this clipping action is progressively more
severe. In the figure, the input is a decaying sinusoid. The output
evolves from a nearly square waveform at the beginning to a pure sinusoid
at the end. This effect will be well known to anyone who has played an
instrument through an overdriven amplifier. The louder the input, the
more distorted will be the output. For this reason, waveshaping is also sometimes
called
distortion.
amounts to a
clipping function. This example shows clearly how the input
amplitude--the index--can
affect the output waveform. The clipping function passes its input
to the output unchanged as long as it stays in the interval between -0.3 and
+0.3. So when the input (in this case a sinusoid) does not exceed 0.3 in
absolute value, the output is the same as the input. But when the input grows
past the 0.3 limit, it is limited to 0.3; and as the amplitude of the
signal increases the effect of this clipping action is progressively more
severe. In the figure, the input is a decaying sinusoid. The output
evolves from a nearly square waveform at the beginning to a pure sinusoid
at the end. This effect will be well known to anyone who has played an
instrument through an overdriven amplifier. The louder the input, the
more distorted will be the output. For this reason, waveshaping is also sometimes
called
distortion.
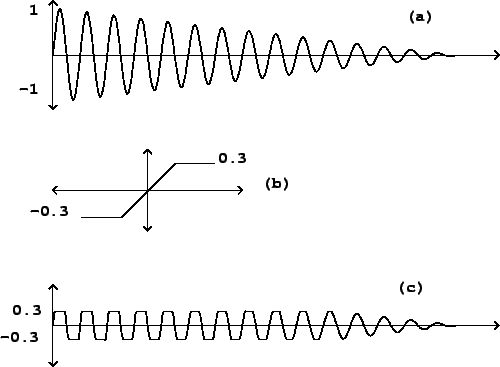 |
Figure 5.7 shows a much simpler and easiest to analyse situation,
in which the transfer function simply squares the input:
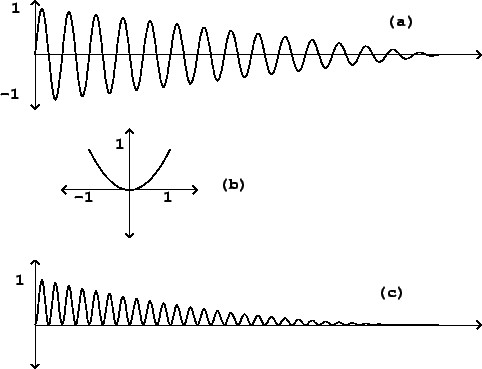 |
Keeping the same transfer function, we now consider the effect of sending in a
combination of two sinusoids with amplitudes ![]() and
and ![]() , and angular
frequencies
, and angular
frequencies ![]() and
and ![]() . For simplicity, we'll omit the initial phase
terms. We set:
. For simplicity, we'll omit the initial phase
terms. We set:
As compared to ring modulation, which is a linear function of its input signal, waveshaping is nonlinear. While we were able to analyze linear processes by considering their action separately on all the components of the input, in this nonlinear case we also have to consider the interactions between components. The results are far more complex--sometimes sonically much richer, but, on the other hand, harder to understand or predict.
In general, we can show that a periodic input, no matter how complex, will
repeat at the same period: if the period is ![]() so that
so that
Combinations of periodic tones at consonant intervals give rise to distortion
products at subharmonics. For instance, if two periodic signals ![]() and
and ![]() are a musical fourth apart (periods in the ratio 4:3), then the sum of the
two repeats at the lower rate given by the common subharmonic. In equations
we would have:
are a musical fourth apart (periods in the ratio 4:3), then the sum of the
two repeats at the lower rate given by the common subharmonic. In equations
we would have:
To get a somewhat more explicit analysis of the effect of waveshaping on
an incoming signal, it is sometimes useful to write the function ![]() as
a finite or infinite power series:
as
a finite or infinite power series:
The individual terms' spectra can be found by applying the cosine product
formula repeatedly:
The negative-frequency terms (which have been shown separately here for clarity) are to be combined with the positive ones; the spectral envelope is folded into itself in the same way as in the ring modulation example of Figure 5.4.
As long as the coefficients ![]() are all positive numbers or zero, then so
are all the amplitudes of the sinusoids in the expansions above. In this
case all the phases stay coherent as
are all positive numbers or zero, then so
are all the amplitudes of the sinusoids in the expansions above. In this
case all the phases stay coherent as ![]() varies and so we get a widening
of the spectrum (and possibly a drastically increasing amplitude) with
increasing values of
varies and so we get a widening
of the spectrum (and possibly a drastically increasing amplitude) with
increasing values of ![]() . On the other hand, if some of the
. On the other hand, if some of the ![]() are
positve and others negative, the different expansions will interfere
destructively; this will give a more complicated-sounding spectral evolution.
are
positve and others negative, the different expansions will interfere
destructively; this will give a more complicated-sounding spectral evolution.
Note also that the successive expansions all contain only even or only odd
partials. If the transfer function (in series form) happens to contain only
even powers:
Many mathematical tricks have been proposed to use waveshaping to generate specified spectra. It turns out that you can generate pure sinusoids at any harmonic of the fundamental by using a Chebyshef polynomial as a transfer function [Leb79], and from there you can go on to build any desired static spectrum (example 5.5.4 demonstrates this.) Generating families of spectra by waveshaping a sinusoid of variable amplitude turns out to be trickier, although several interesting special cases have been found, one of which is developed here in chapter [].