




Next: Periodic Signals
Up: Sinusoids, amplitude and frequency
Previous: Synthesizing a Sinusoid
Contents
Index
Superposing Signals
If a signal ![$x[n]$](img78.png) has a peak or RMS amplitude
has a peak or RMS amplitude 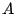 (in some fixed window), then
the scaled signal
(in some fixed window), then
the scaled signal ![$k \cdot a[n]$](img114.png) (where
(where 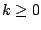 ) has amplitude
) has amplitude 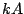 . The
RMS power of the scaled signal changes by a factor of
. The
RMS power of the scaled signal changes by a factor of 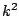 . The situation gets
more complicated when two different signals are added together; just knowing
the amplitudes of the two does not suffice to know the amplitude of the sum.
The two amplitude measures do at least obey triangle inequalities; for any
two signals
. The situation gets
more complicated when two different signals are added together; just knowing
the amplitudes of the two does not suffice to know the amplitude of the sum.
The two amplitude measures do at least obey triangle inequalities; for any
two signals ![$x[n]$](img78.png) and
and ![$y[n]$](img1.png) ,
,
If we fix a window from 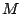 to
to 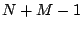 as usual, we can write out the
mean power of the sum of two signals:
as usual, we can write out the
mean power of the sum of two signals:
where we have introduced the correlation of two signals:
Correlation
The correlation may be positive, zero, or negative. Over a sufficiently large
window, the correlation of two Sinusoids with different frequencies is
negligible. In general, for two uncorrelated signals, the power of the
sum is the sum of the powers:
Put in terms of amplitude, this becomes:
This is the familiar Pythagorean relation. So uncorrelated signals can be
thought of as vectors at right angles to each other; positively correlated ones
as having an acute angle between them, and negatively correlated as having an
obtuse angle between them.
For example, if two uncorrelated signals both have RMS amplitude 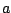 ,
the sum will have RMS amplitude
,
the sum will have RMS amplitude 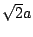 . On the other hand if the two
signals happen to be equal--the most correlated possible--the sum will have
amplitude
. On the other hand if the two
signals happen to be equal--the most correlated possible--the sum will have
amplitude 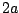 , which is the maximum allowed by the triangle inequality.
, which is the maximum allowed by the triangle inequality.





Next: Periodic Signals
Up: Sinusoids, amplitude and frequency
Previous: Synthesizing a Sinusoid
Contents
Index
Miller Puckette
2006-03-03
![]() has a peak or RMS amplitude
has a peak or RMS amplitude ![]() (in some fixed window), then
the scaled signal
(in some fixed window), then
the scaled signal ![]() (where
(where ![]() ) has amplitude
) has amplitude ![]() . The
RMS power of the scaled signal changes by a factor of
. The
RMS power of the scaled signal changes by a factor of ![]() . The situation gets
more complicated when two different signals are added together; just knowing
the amplitudes of the two does not suffice to know the amplitude of the sum.
The two amplitude measures do at least obey triangle inequalities; for any
two signals
. The situation gets
more complicated when two different signals are added together; just knowing
the amplitudes of the two does not suffice to know the amplitude of the sum.
The two amplitude measures do at least obey triangle inequalities; for any
two signals ![]() and
and ![]() ,
,
![]() ,
the sum will have RMS amplitude
,
the sum will have RMS amplitude ![]() . On the other hand if the two
signals happen to be equal--the most correlated possible--the sum will have
amplitude
. On the other hand if the two
signals happen to be equal--the most correlated possible--the sum will have
amplitude ![]() , which is the maximum allowed by the triangle inequality.
, which is the maximum allowed by the triangle inequality.