Synthesizing a Sinusoid

In most widely used audio synthesis and processing packages (Csound, Max/MSP, and Pd, for instance), the audio operations are specified as networks of unit generators[Mat69] which pass audio signals among themselves. The user of the software package specifies the network, sometimes called a patch, which essentially corresponds to the synthesis algorithm to be used, and then worries about how to control the various unit generators in time. In this section, we'll use abstract block diagrams to describe patches, but in the ``examples" section (page ), we'll to choose a specific implementation environment and show some of the software-dependent details.

To show how to produce a Sinusoid with time-varying amplitude we'll need to introduce two unit generators. First we need a pure Sinusoid which is made with an oscillator. Figure 1.4(a) shows the icon for a sinusoidal oscillator. The input is a frequency (in cycles per second), and the output is a Sinusoid of peak amplitude one.

Figure 1.4: Block diagrams for (a) a sinusoidal oscillator; (b) controlling the amplitude using a multiplier and an amplitude signal $y[n]$.

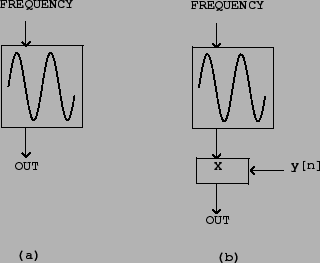Figure 1.4(b) shows how to multiply the output of a sinusoidal oscillator by an appropriate amplitude scaler $y[n]$ to control its amplitude. Since the oscillator's peak amplitude is 1, the peak amplitude of the product is about $y[n]$, assuming $y[n]$ changes slowly enough and doesn't become negative in value.

Figure 1.5: Two amplitude functions (a, c), and, in (b) and (d), the result of multiplying them by the pure Sinusoid of Figure 1.1.

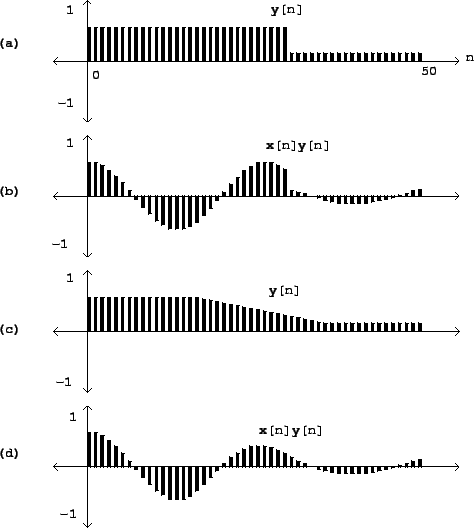Figure 1.5 shows how the Sinusoid of Figure 1.1 is affected by amplitude change by two different controlling signals $y[n]$. The controlling signal shown in part (a) has a discontinuity, and so therefore does the resulting amplitude-controlled sinusoid shown in (b). Parts c and d show a more gently-varying possibility for $y[n]$ and the result. Intuition suggests that the result shown in (b) won't sound like an amplitude-varying sinusoid, but instead like a sinusoid interrupted by a fairly loud ``pop" after which it continues more quietly. In general, for reasons that can't be explained in this chapter, amplitude control signals $y[n]$ which ramp smoothly from one value to another are less likely to give rise to parasitic results (such as that ``pop") than are abruptly changing ones.

For now we can state two general rules without justifying them. First, pure Sinusoids are the class of signals most sensitive to the parasitic effects of quick amplitude change. So when you want to test an amplitude transition, if it works for Sinusoids it will probably work for other signals as well. Second, depending on the signal whose amplitude you are changing, the amplitude control will need between 0 and 30 milliseconds of ``ramp" time--zero for the most forgiving signals (such as white noise), and 30 for the least (such as a Sinusoid). All this also depends in a complicated way on listening levels and the acoustic context.

Suitable amplitude control functions $y[n]$ may be obtained using an envelope generator. Figure 1.6 shows a network in which an envelope generator is used to control the amplitude of an oscillator. Envelope generators vary widely in functionality from one design to another, but we will focus on the simplest kind, which generates line segments as shown in fig. 1.4(b). If a line segment is specified to ramp between two output values $a$ and $b$ over $N$ samples starting at sample number $M$, the output is:

$$y[n] = a + (b - a) {{n-M} \over N}, \hspace{0.1in} M \le n \le M+N-1.$$

The output may have any number of segments such as this, laid end to end, over the entire range of sample numbers $n$; flat, horizontal segments can be made by setting $a=b$.

Figure 1.6: Using an envelope generator to control amplitude.

In addition to changing amplitudes of sounds, amplitude control is often used, expecially in real-time applications, simply to turn sounds on and off: to turn one off, ramp the amplitude smoothly to zero. Most software synthesis packages also provide ways to actually stop modules from computing samples at all, but here we'll use amplitude control instead.

Envelope generators are described in more detail in section 4.1.