




Next: Time shifts and phase
Up: Complex numbers
Previous: Complex numbers
Contents
Index
Recall the formula for a (real-valued) sinusoid from page
![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) :
:
This is a sequence of cosines of angles (called phases) which increase
arithmetically
with the sample number 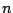 . The cosines are all adjusted by the factor
. The cosines are all adjusted by the factor 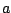 .
We can now re-write this as the real part of a much simpler and easier to
manipulate sequence of complex numbers, by using the properties of their
arguments and magnitudes.
.
We can now re-write this as the real part of a much simpler and easier to
manipulate sequence of complex numbers, by using the properties of their
arguments and magnitudes.
Suppose that our complex number 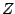 happens to have magnitude one, so that
it can be written as:
happens to have magnitude one, so that
it can be written as:
Then for any integer 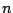 , the number
, the number 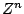 must have magnitude one as well
(because magnitudes multiply) and argument
must have magnitude one as well
(because magnitudes multiply) and argument 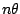 (because arguments add).
So,
(because arguments add).
So,
This is also true for negative values of 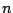 , so for example,
, so for example,
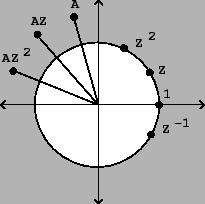
Figure 7.2 shows graphically how the powers of 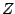 wrap around
the unit circle, which is the set of all complex numbers of magnitude one.
They form a geometric sequence:
wrap around
the unit circle, which is the set of all complex numbers of magnitude one.
They form a geometric sequence:
and taking the real part of each term we get a real sinusoid with
initial phase zero and amplitude one:
The sequence of complex numbers is much easier to manipulate algebraically
than the sequence of cosines.
Figure 7.2:
The powers of a complex number 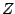 with
with 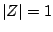 , and the same
sequence multiplied by a constant
, and the same
sequence multiplied by a constant 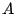 .
.
 |
Furthermore, suppose we multiply the elements of the sequence by some (complex)
constant 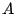 with magnitude
with magnitude 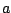 and argument
and argument 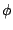 . This gives
. This gives
The magnitudes are all 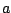 and the argument of the
and the argument of the 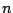 th term is
th term is
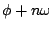 , so the sequence is equal to
, so the sequence is equal to
and so the real part is just the real-valued sinusoid:
The complex amplitude 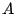 encodes both the amplitude (equal to its magnitude
encodes both the amplitude (equal to its magnitude 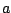 )
and the inital phase (its argument
)
and the inital phase (its argument 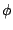 ); the unit-magnitude complex
number
); the unit-magnitude complex
number 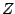 controls the frequency which is just its argument
controls the frequency which is just its argument 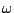 .
.
Figure 7.2 also shows the sequence
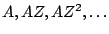 ;
in effect this is the same sequence as
;
in effect this is the same sequence as
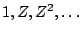 , but amplified and
rotated according to the amplitude and initial phase. In a complex
sinusoid of this form,
, but amplified and
rotated according to the amplitude and initial phase. In a complex
sinusoid of this form, 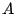 is called the
complex amplitude.
is called the
complex amplitude.
Using complex numbers to represent the amplitudes and phases of sinusoids
can clarify manipulations that otherwise might seem unmotivated. For instance,
in Section ![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) we looked at the sum of two sinusoids with
the same frequency. In the language of this chapter, we let the two
sinusoids be written as:
we looked at the sum of two sinusoids with
the same frequency. In the language of this chapter, we let the two
sinusoids be written as:
where 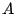 and
and 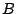 encode the phases and amplitudes of the two signals.
The sum is then equal to:
encode the phases and amplitudes of the two signals.
The sum is then equal to:
which is a sinusoid whose amplitude equals 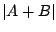 and whose phase equals
and whose phase equals
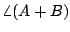 . This is clearly a much easier way to manipulate amplitudes
and phases than using series of sines and cosines. Eventually, of course,
we will take the real part of the result; this can usually be left to the
very last step of the calculation.
. This is clearly a much easier way to manipulate amplitudes
and phases than using series of sines and cosines. Eventually, of course,
we will take the real part of the result; this can usually be left to the
very last step of the calculation.





Next: Time shifts and phase
Up: Complex numbers
Previous: Complex numbers
Contents
Index
Miller Puckette
2006-03-03
![]() :
:
![]() happens to have magnitude one, so that
it can be written as:
happens to have magnitude one, so that
it can be written as:
![]() with magnitude
with magnitude ![]() and argument
and argument ![]() . This gives
. This gives
![]() ;
in effect this is the same sequence as
;
in effect this is the same sequence as
![]() , but amplified and
rotated according to the amplitude and initial phase. In a complex
sinusoid of this form,
, but amplified and
rotated according to the amplitude and initial phase. In a complex
sinusoid of this form, ![]() is called the
complex amplitude.
is called the
complex amplitude.
![]() we looked at the sum of two sinusoids with
the same frequency. In the language of this chapter, we let the two
sinusoids be written as:
we looked at the sum of two sinusoids with
the same frequency. In the language of this chapter, we let the two
sinusoids be written as: