Shifts and phase changes

Section 7.2 showed how time-shifting a signal changes the phases of its sinusoidal components, and section 8.4.3 showed how multiplying a signal by a complex sinusoid shifts its component frequencies. These two effects each correspond to an identity involving the Fourier transform.

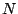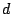First we consider a time shift. If $X[n]$, as usual, is a complex-valued signal that repeats every $N$ samples, let $Y[n]$ be $X[n]$ delayed $d$ samples:

$$Y[n] = X[n-d]$$

which also repeats every 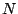$N$ samples since 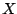$X$ does. We can reduce the Fourier transform of $Y[n]$ this way:

$${\cal FT} \left \{ Y[n] \right \} (k) = {V ^ {0}} Y[0] + {V ^ {1}} Y[1] + \cdots + {V ^ {N-1}} Y[N-1]$$

$$= {V ^ {0}} X[-d] + {V ^ {1}} X[-d+1] + \cdots + {V ^ {N-1}} X[-d+N-1]$$

$$= {V ^ {d}} X[0] + {V ^ {d+1}} X[1] + \cdots + {V ^ {d+N-1}} X[N-1]$$

$$= {V^d} \left ( {V ^ {d}} X[0] + {V ^ {d+1}} X[1] + \cdots + {V ^ {d+N-1}} X[N-1] \right )$$

$$= {V^d} {\cal FT} \left \{ X[n] \right \} (k)$$

We therefore get the TIME SHIFT FORMULA FOR FOURIER TRANSFORMS:

$${\cal FT} \left \{ Y[n] \right \} (k) = \left (\cos(-dk\o... ...sin(-dk\omega) \right ) {\cal FT} \left \{ X[n] \right \} (k)$$

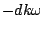So the Fourier transform of $Y[n]$ is a phase term times the Fourier transform of $X[n]$. The phase is changed by $-dk\omega$, a multiple of the frequency $k$.

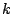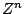Now suppose instead that we change our starting signal $X[n]$ by multiplying it by a complex exponential $Z^n$ with angular frequency $\alpha$:

$$Y[n] = {Z^n} X[n]$$

$$Z = \cos(\alpha) + i \sin(\alpha)$$

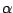The Fourier transform is:

$${\cal FT} \left \{ Y[n] \right \} (k) = {V ^ {0}} Y[0] + {V ^ {1}} Y[1] + \cdots + {V ^ {N-1}} Y[N-1]$$

$$= {V ^ {0}} X[0] + {V ^ {1}} Z X[1] + \cdots + {V ^ {N-1}} {Z^{N-1}} X[N-1]$$

$$= {{(VZ)} ^ {0}} X[0] + {{(VZ)} ^ {1}} X[1] + \cdots + {{(VZ)} ^ {N-1}} X[N-1]$$

$$= {\cal FT} \left \{ X[n] \right \} (k + {{\alpha } \over {\omega}})$$

We therefore get the PHASE SHIFT FORMULA FOR FOURIER TRANSFORMS:

$${\cal FT} \left \{ (\cos(\alpha) + i \sin(\alpha)) X[n] \ri... ...l FT} \left \{ X[n] \right \} (k + {{\alpha N} \over {2 \pi}})$$