




Next: Shifts and phase changes
Up: Properties of Fourier transforms
Previous: Properties of Fourier transforms
Contents
Index
Now let ![$X[n]=1$](img1103.png) for all
for all 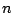 (this repeats with any desired integer period
(this repeats with any desired integer period
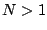 ). From the preceding discussion, we expect to find that
). From the preceding discussion, we expect to find that
We will often need to know the answer for non-integer values of 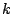 however,
and for this there is nothing better to do than to calculate the value
directly:
however,
and for this there is nothing better to do than to calculate the value
directly:
where 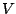 (which depends on
(which depends on 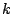 ) is as before. This is a geometric
sum, and as long as
) is as before. This is a geometric
sum, and as long as 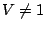 we get:
we get:
We now symmetrize the top and bottom in the same way as we earlier did in
Section 7.3. To do this let:
so that 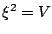 . Then taking appropriate powers of
. Then taking appropriate powers of 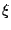 out of the
numerator and denominator gives:
out of the
numerator and denominator gives:
It's easy now to simplify the numerator:
and similarly for the denominator, giving:
Putting it all together, whether 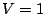 or not, we have
or not, we have
where 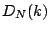 , known as the
Dirichlet kernel,
is defined as
, known as the
Dirichlet kernel,
is defined as
Figure 9.1 shows the Fourier transform of ![$X[n]$](img692.png) , with
, with 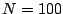 . The
transform repeats every 100 samples, with a peak at
. The
transform repeats every 100 samples, with a peak at 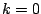 , another at
, another at
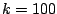 , and so on. The figure endeavors to show both the magnitude and phase
behavior using a 3-dimensional graph projected onto the page. The phase
term
, and so on. The figure endeavors to show both the magnitude and phase
behavior using a 3-dimensional graph projected onto the page. The phase
term
acts to twist the values of
![${\cal FT} \left \{ X[n] \right \} (k)$](img1121.png) around
the
around
the 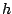 axis with a period of approximately two. The Dirichlet kernel
axis with a period of approximately two. The Dirichlet kernel
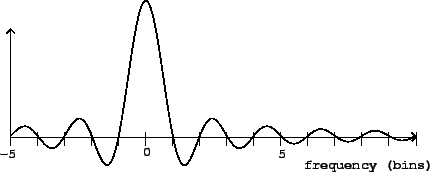
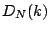 , shown in Figure 9.2, controls the magnitude of
, shown in Figure 9.2, controls the magnitude of
![${\cal FT} \left \{ X[n] \right \} (k)$](img1121.png) . It has a peak, two bins wide, around
. It has a peak, two bins wide, around
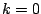 . This is surrounded by one-bin-wide
sidelobes,
alternating in sign and gradually decreasing in magnitude as
. This is surrounded by one-bin-wide
sidelobes,
alternating in sign and gradually decreasing in magnitude as 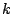 increases or
decreases away from zero. The phase term rotates by almost
increases or
decreases away from zero. The phase term rotates by almost 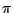 radians
each time the Dirichlet kernel changes sign, so that the product of the
two stays roughly in the same complex half-plane for
radians
each time the Dirichlet kernel changes sign, so that the product of the
two stays roughly in the same complex half-plane for 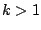 (and in the
opposite half-plane for
(and in the
opposite half-plane for 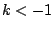 ). The phase rotates by about
). The phase rotates by about 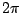 radians over the peak from
radians over the peak from 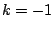 to
to 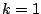 .
.
Figure 9.1:
The Fourier transform of a signal consisting of all ones. Here
N=100, and values are shown for 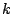 ranging from -5 to 10. The result
is complex-valued and shown as a projection, with the real axis pointing up the
page and the imaginary axis pointing away from it.
ranging from -5 to 10. The result
is complex-valued and shown as a projection, with the real axis pointing up the
page and the imaginary axis pointing away from it.
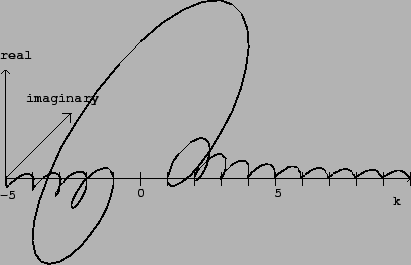 |
Figure 9.2:
The Dirichlet kernel, for 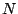 = 100.
= 100.
 |





Next: Shifts and phase changes
Up: Properties of Fourier transforms
Previous: Properties of Fourier transforms
Contents
Index
Miller Puckette
2006-03-03
![]() for all
for all ![]() (this repeats with any desired integer period
(this repeats with any desired integer period
![]() ). From the preceding discussion, we expect to find that
). From the preceding discussion, we expect to find that
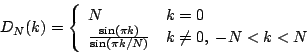
![]() , with
, with ![]() . The
transform repeats every 100 samples, with a peak at
. The
transform repeats every 100 samples, with a peak at ![]() , another at
, another at
![]() , and so on. The figure endeavors to show both the magnitude and phase
behavior using a 3-dimensional graph projected onto the page. The phase
term
, and so on. The figure endeavors to show both the magnitude and phase
behavior using a 3-dimensional graph projected onto the page. The phase
term
