




Next: Pulse trains via wavetable
Up: Pulse trains
Previous: Pulse trains
Contents
Index
In the ring modulated waveshaping formulation,
the shape of the formant is determined by
a modulation term
For small values of the index 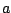 , the modulation term varies only slightly from
the constant value
, the modulation term varies only slightly from
the constant value 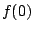 , so most of the energy is concentrated at DC.
As
, so most of the energy is concentrated at DC.
As 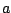 increases, the energy spreads out among progressively higher harmonics
of the fundamental
increases, the energy spreads out among progressively higher harmonics
of the fundamental 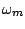 . Depending on the function
. Depending on the function 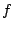 , this spread
may be orderly or disorderly. An orderly spread may be desirable and
then again may not, depending on whether our goal is a predictable spectrum or
a wide range of different (and perhaps hard-to-predict) spectra.
, this spread
may be orderly or disorderly. An orderly spread may be desirable and
then again may not, depending on whether our goal is a predictable spectrum or
a wide range of different (and perhaps hard-to-predict) spectra.
A waveshaping function that gives well-behaved, simple and predictable results
was already developed in
section 5.5.5. Using the function
and normalizing suitably,
we get the spectra shown in figure 5.13. A slight rewriting of the
waveshaping modulator for this choice of 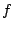 (and taking the renormalization
into account) gives:
(and taking the renormalization
into account) gives:
where 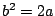 so that
so that 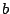 is proportional to the bandwidth. This can
be rewritten as
is proportional to the bandwidth. This can
be rewritten as
Except for a missing normalization factor, this is a Gaussian distribution,
sometimes called a ``bell curve". The amplitudes of the harmonics are
given by Bessel ``I" type functions.
Another good choice is the (again unnormalized) Cauchy distribution:
which gives rise to a spectrum of exponentially falling harmonics:
where 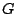 and
and 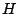 are functions of the index
are functions of the index 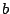 (exact formulas are given in [Puc95a]).
(exact formulas are given in [Puc95a]).
In both this and the Gaussian case above, the bandwidth (counted in peaks,
i.e., units of 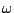 ) is roughly proportional to the index
) is roughly proportional to the index 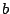 , and the
amplitude of the DC term (the peak of the spectrum) is roughly proportional
to
, and the
amplitude of the DC term (the peak of the spectrum) is roughly proportional
to 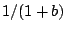 .
For either waveshaping function (
.
For either waveshaping function (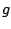 or
or 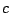 ), if
), if 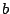 is larger than about 2,
the waveshape of
is larger than about 2,
the waveshape of
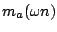 is
approximately a (forward or backward) scan of the transfer function, and so
this and the earlier example (the ``wavetable formulation") both look
like pulses whose widths decrease as the specified bandwidth increases.
is
approximately a (forward or backward) scan of the transfer function, and so
this and the earlier example (the ``wavetable formulation") both look
like pulses whose widths decrease as the specified bandwidth increases.
Before considering more complicated carrier signals to go with the modulators
we've seen so far, it is instructive to see what multiplication by a pure
sinusoid gives us as waveforms and spectra. Figure 6.5 shows
the result of multiplying two different pulse trains by a sinusoid at the
sixth partial:
where the index of modulation 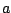 is two in both cases. In part (a)
is two in both cases. In part (a) 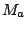 is
the stretched Hanning windowing function; part (b)
shows waveshaping via the unnormalized Cauchy distribution. One period
of each waveform is shown.
is
the stretched Hanning windowing function; part (b)
shows waveshaping via the unnormalized Cauchy distribution. One period
of each waveform is shown.





Next: Pulse trains via wavetable
Up: Pulse trains
Previous: Pulse trains
Contents
Index
Miller Puckette
2006-03-03
![]() ) is roughly proportional to the index
) is roughly proportional to the index ![]() , and the
amplitude of the DC term (the peak of the spectrum) is roughly proportional
to
, and the
amplitude of the DC term (the peak of the spectrum) is roughly proportional
to ![]() .
For either waveshaping function (
.
For either waveshaping function (![]() or
or ![]() ), if
), if ![]() is larger than about 2,
the waveshape of
is larger than about 2,
the waveshape of
![]() is
approximately a (forward or backward) scan of the transfer function, and so
this and the earlier example (the ``wavetable formulation") both look
like pulses whose widths decrease as the specified bandwidth increases.
is
approximately a (forward or backward) scan of the transfer function, and so
this and the earlier example (the ``wavetable formulation") both look
like pulses whose widths decrease as the specified bandwidth increases.