




Next: Resulting spectra
Up: Pulse trains
Previous: Pulse trains via waveshaping
Contents
Index
In the wavetable formulation, the pulse train can be made by a stretched
wavetable:
where
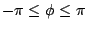 is the phase. The function
is the phase. The function 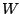 should be zero at
and beyond the points
should be zero at
and beyond the points 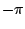 and
and 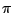 , and rise to a maximum at 0. A possible
choice for the function
, and rise to a maximum at 0. A possible
choice for the function 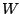 is
is
which is graphed in part (a) of Figure 6.4. This is known as the
Hanning window function;
it will come up again
in chapter 9.
Figure:
Pulse width modulation using the Hanning window function: a. the
function
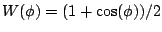 ; b. the function repeated at a duty
cycle of 100% (modulation index
; b. the function repeated at a duty
cycle of 100% (modulation index 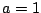 ); c. the function at a 50% duty
cycle (
); c. the function at a 50% duty
cycle (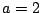 ).
).
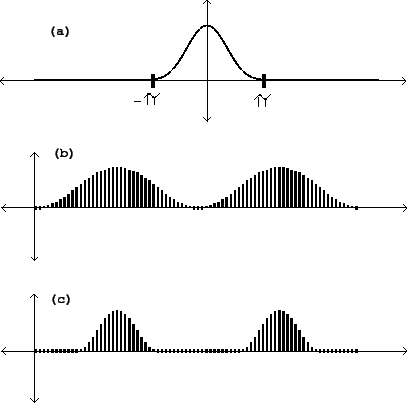 |
Realizing this as a repeating waveform, we get a succession of (appropriately
sampled) copies of the function 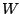 , whose duty cycle is
, whose duty cycle is
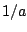 (parts b and c of the figure).
If you don't wish the copies to overlap we require
(parts b and c of the figure).
If you don't wish the copies to overlap we require 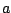 to be
at least 1. If you want overlap the best strategy is to
duplicate the block diagram (Figure 6.3) out of phase, as described
in Section 2.4 and realized in Section
2.6.5.
to be
at least 1. If you want overlap the best strategy is to
duplicate the block diagram (Figure 6.3) out of phase, as described
in Section 2.4 and realized in Section
2.6.5.





Next: Resulting spectra
Up: Pulse trains
Previous: Pulse trains via waveshaping
Contents
Index
Miller Puckette
2006-03-03

![]() , whose duty cycle is
, whose duty cycle is
![]() (parts b and c of the figure).
If you don't wish the copies to overlap we require
(parts b and c of the figure).
If you don't wish the copies to overlap we require ![]() to be
at least 1. If you want overlap the best strategy is to
duplicate the block diagram (Figure 6.3) out of phase, as described
in Section 2.4 and realized in Section
2.6.5.
to be
at least 1. If you want overlap the best strategy is to
duplicate the block diagram (Figure 6.3) out of phase, as described
in Section 2.4 and realized in Section
2.6.5.