




Next: Fourier transform of a
Up: Properties of Fourier transforms
Previous: Fourier transform of DC
Contents
Index
Shifts and phase changes
Section 7.2 showed how time-shifting a signal changes the
phases of its sinusoidal components, and Section 8.4.3
showed how multiplying a signal by a complex sinusoid shifts its component
frequencies. These two effects have corresponding identities
involving the Fourier transform.
First we consider a time shift. If ![$X[n]$](img668.png) , as usual, is a complex-valued
signal that repeats every
, as usual, is a complex-valued
signal that repeats every 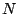 samples, let
samples, let ![$Y[n]$](img716.png) be
be ![$X[n]$](img668.png) delayed
delayed 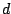 samples:
samples:
which also repeats every 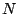 samples since
samples since 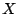 does. We can reduce the Fourier
transform of
does. We can reduce the Fourier
transform of ![$Y[n]$](img716.png) this way:
this way:
(The third line is just the second one with the terms summed in a
different order). We therefore get the Time Shift Formula for Fourier
Transforms:
So the Fourier transform of ![$X[n-d]$](img1104.png) is a phase term times the Fourier transform
of
is a phase term times the Fourier transform
of ![$X[n]$](img668.png) . The phase is changed by
. The phase is changed by 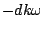 , a
linear function of the frequency
, a
linear function of the frequency 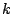 .
.
Now suppose instead that we change our starting signal ![$X[n]$](img668.png) by multiplying
it by a complex exponential
by multiplying
it by a complex exponential 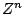 with angular frequency
with angular frequency 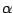 :
:
The Fourier transform is:
We therefore get the Phase Shift Formula for Fourier Transforms:





Next: Fourier transform of a
Up: Properties of Fourier transforms
Previous: Fourier transform of DC
Contents
Index
Miller Puckette
2006-09-24
![]() , as usual, is a complex-valued
signal that repeats every
, as usual, is a complex-valued
signal that repeats every ![]() samples, let
samples, let ![]() be
be ![]() delayed
delayed ![]() samples:
samples:
![]() by multiplying
it by a complex exponential
by multiplying
it by a complex exponential ![]() with angular frequency
with angular frequency ![]() :
: