- 6.3.1 ... As a Function of Space
- 6.3.2 ... As a Function of Time
- 6.3.3 ... as a Function of
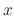 and
and 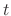
- 6.3.4 Directional Waves as Superpositions of Plane Waves
Up to now we have dealt with signals and recordings, and ignored the phenomenon of sound itself. But unless you are using headphones to listen to a purely electronic signal, there will be one or more stages in any chain of audio production that is mediated by real, acoustic, in-the-air sound. There is much to know about how sound is propagated through the air and how objects absorb, reflect, and emit sounds. In the context of this course we will only have room and time for the very basics.
Air has mass, and it also acts as a spring--it can be compressed by applying force. Like any mass-and-spring system, it is able to store and transmit energy in the form of vibrations. In the particular case of air, these vibrations move in waves from one place to another. There are two kinds of variables to be concerned with: variations in air pressure from place to place and over time, and physical displacement of the air itself. At a given point in space and time, the pressure is a number in units of force per area (for instance, Newtons per square meter). One almost always speaks of the pressure as being positive if it is greater than atmospheric pressure, and negative if it is less - in other words, we tacitly subtract one atmosphere from the variables we use for pressure.
The displacement is a vector; it has magnitude and direction. When the air is at rest the displacement is zero. When sound is present, the displacement changes with time and as a result the air also has a non-zero velocity that can be calculated from the displacement as a function of time.
One can idealize sound as having a source, and as traveling through the air to the point at which we hear or measure it. If a listener or microphone is distant enough from the source, the chain of transmission through the air can be thought of as shown:
![\includegraphics[bb = 103 272 507 525, scale=0.6]{fig/F01-near-far.ps}](img171.png)
The sound first passes through an area called the near field, in which the strength and even the direction the sound is traveling in might vary from point to point. If, however, we go out to a distance several times the size of the source, we can say approximately that the sound is moving unidirectionally. The pressure, displacement, and velocity of the air depend (approximately) only on one dimension, in the direction from the source to the listener. If the listener moves in a perpendicular direction to that axis, the sound is (approximately) unchanged.
Sound travels at some 343 meters per second (in the air, at sea level; this
varies slightly with temperature and altitude). In English units this is
about 767 miles per hour, or 1167 feet per second, or, in very round numbers,
about one foot per millisecond. This is the
velocity of sound which we'll call ![]() .
.
If the source and listener are separated
by a distance ![]() , the sound arrives at the listener with a delay
, the sound arrives at the listener with a delay
![]() .
If the delay
.
If the delay ![]() is known, the distance can be found using
is known, the distance can be found using ![]() .
.
If the source and/or the listener is moving in space so that the distance between the two is changing, then the delay between the source and the listener changes as well. This results in a speeding up or slowing down of the sound.
To see this in detail, suppose the distance is changing at a speed ![]() , measured
in units of distance per time as is proper for a velocity. Then over a period
of time
, measured
in units of distance per time as is proper for a velocity. Then over a period
of time ![]() the distance changes by
the distance changes by ![]() and the time of transmission by
and the time of transmission by
![]() . So the receiver receives the emitted sound not in time
. So the receiver receives the emitted sound not in time ![]() ,
but in an amount of time that is changed by
,
but in an amount of time that is changed by ![]() . The time
overall over which the sound of length
. The time
overall over which the sound of length ![]() arrives is thus:
arrives is thus:
The pressure is a simpler variable to deal with than the
velocity, and the simplest measure of the strength of a sound is a measure of
power derived from the pressure. If, at a point in space, the pressure is
a function of time ![]() , the
effective sound pressure
at that point is the root mean square of
, the
effective sound pressure
at that point is the root mean square of ![]() , that is, the square root
of the average of
, that is, the square root
of the average of ![]() . This is usually put in units of decibels and
called the
sound pressure level or
SPL for short. To do so we need a reference value which is conventionally set
at 0.00002 (20 millionths) newtons per square meter, which is roughly the
quietest sound that would be audible under ideal conditions (the threshold of
human hearing at 1 kHz). Thus if the RMS sound pressure is
. This is usually put in units of decibels and
called the
sound pressure level or
SPL for short. To do so we need a reference value which is conventionally set
at 0.00002 (20 millionths) newtons per square meter, which is roughly the
quietest sound that would be audible under ideal conditions (the threshold of
human hearing at 1 kHz). Thus if the RMS sound pressure is ![]() , the SPL is
, the SPL is
It is often useful to know how the SPL of a sound relates to the power of the
sound at its source and the distance from the source to the listener. To do
this we need a measure of how much power a unidirectional sound carries as a
function of its SPL. This power flow (sometimes called the
intensity, which we'll denote by ![]() ) is in
units of power per unit area, for instance, watts per square meter.
(Caveat: there appear to be conflicting definitions of intensity; see for
instance Wikipedia).
To find
) is in
units of power per unit area, for instance, watts per square meter.
(Caveat: there appear to be conflicting definitions of intensity; see for
instance Wikipedia).
To find ![]() requires a more complicated calculation than
can reasonably be presented here, but the upshot (for an ideal gas at least) is
this:
requires a more complicated calculation than
can reasonably be presented here, but the upshot (for an ideal gas at least) is
this:
![\includegraphics[bb = 139 245 501 548, scale=0.6]{fig/F02-sphere.ps}](img192.png)
So the intensity (power flow) is
Since, at least when we're not too close to the source (and still not
considering issues such as deflections by other objects), the sound is roughly
moving unidirectionally, it is useful to study unidirectional waves before
studying more complicated ones. It is natural to start with sinusoids. A
mathematical construct called the
plane wave
(but perhaps better described more explicitly as a
sinusoidal plane wave), is a sound whose pressure changes sinusoidally at
each point in space (so that a microphone would pick up a sinusoid), and that
has a fixed direction. Three parameters (an amplitude, a frequency, and a
direction in space) determine a plane wave completely. For simplicity, we'll
choose a fixed direction, along the ![]() axis to the right. The plane wave's
pressure, as a function of time and space, can be written as:
axis to the right. The plane wave's
pressure, as a function of time and space, can be written as:
The independent variables ![]() and
and ![]() don't appear in the equation; the pressure
isn't changed if we move in the
don't appear in the equation; the pressure
isn't changed if we move in the ![]() or
or ![]() direction.
direction.
We now look at the plane wave's shape at an instant in time, say ![]() .
At that moment the plane wave is a function of three spatial dimensions (but
only depends on one of them):
.
At that moment the plane wave is a function of three spatial dimensions (but
only depends on one of them):
![\includegraphics[bb = 83 144 509 660, scale=0.6]{fig/F03-planes.ps}](img208.png)
We can re-write the plane wave using ![]() in the place of
in the place of ![]() :
:
At a fixed point in space, (but now allowing time to vary), the pressure varies
sinusoidally. We can re-group the original equation for pressure as:
Placing two microphones (say, at points
![]() and
and
![]() will pick up sinusoids whose initial phases differ by
will pick up sinusoids whose initial phases differ by
![]() .
.
For a third point of view, here is a graph of the plane wave as a function of
![]() and
and ![]() , as a three-dimensional surface:
, as a three-dimensional surface:
![\includegraphics[bb = 14 14 612 541, scale=0.5]{fig/f04-3dgraph.ps}](img221.png)
Here the horizontal axis in front shown distance in feet from 0 to 100, and the
other horizontal axis (running from front to back in perspective) shows time
from 0 to 0.1 second. To keep the numbers round, the speed of sound was
rounded off to 1000 feet per second. The wavelength was chosen as 20 feet,
corresponding to a frequency of 50 Hz.
There are crests separated in space by ![]() 20 feet), and in time by
20 feet), and in time by
![]() 1/50 of a second.
1/50 of a second.
The locations of the crests form a series of parallel lines defined by setting
the phase to any multiple of ![]() :
:
![\includegraphics[bb = 87 261 433 527, scale=0.6]{fig/F05-lines.ps}](img219.png)
Over each period ![]() , the crests of the plane wave march forward
, the crests of the plane wave march forward ![]() units of distance, so that each one is replaced by the one in back of it. The
slopes of the lines are all equal to
units of distance, so that each one is replaced by the one in back of it. The
slopes of the lines are all equal to
![]() , which equals
, which equals ![]() .
.
It is an interesting property of sound in the air that (for practical purposes)
plane waves of different frequencies all move a the same speed ![]() . (This
isn't necessarily true in other media, and is quite noticeably not the case
in solids).
. (This
isn't necessarily true in other media, and is quite noticeably not the case
in solids).
To give an idea of the scale of reasonable wavelengths for sound: at 20 Hz. the wavelength is about 50 feet and at 20 kHz, it's about 0.6 inches.
If an arbitrary sound is traveling unidirectionally (say, in the ![]() direction)
it can, theoretically speaking and with some provisos,, be expressed as a
s mixture of a (possibly infinite) number of sinusoidal plane waves, which
correspond to the way its value at one point (a signal) could be written as a
sum of sinusoids. In considering how a unidirectional sound behaves in space,
it suffices to consider how its component sinusoids would behave separately.
direction)
it can, theoretically speaking and with some provisos,, be expressed as a
s mixture of a (possibly infinite) number of sinusoidal plane waves, which
correspond to the way its value at one point (a signal) could be written as a
sum of sinusoids. In considering how a unidirectional sound behaves in space,
it suffices to consider how its component sinusoids would behave separately.
When a unidirectional sound encounters a flat, non-moving surface such as the wall of a room, it is reflected. If the wall is many times larger in both dimensions than one wavelength of the sound, its reflection is also approximately a plane wave. (So, if a sound has many frequency components, it might be observed that the higher frequencies in the sound are reflected roughly as light off a mirror, but that lower frequencies are dispersed in many directions. We'll return to this later; the effect is called diffraction.
Focusing for now on the situation where the reflection may be considered a plane wave (as well as the incident wave), we can describe the whole sound field as a superposition (mixture, or sum) of two plane waves, with equal frequencies and amplitudes but different directions.
We can see how these will interact by considering, at various points in space,
how the phases of the two plane waves compare. Where they're equal, the sound
pressure level will be 6 db higher than that of the incident wave. Wherever they
differ by ![]() , the two will cancel out and you will get silence.
This combination of regions in space having higher and lower amplitudes of sound
present is called an
interference pattern.
In the example we're considering, the situation looks like this:
, the two will cancel out and you will get silence.
This combination of regions in space having higher and lower amplitudes of sound
present is called an
interference pattern.
In the example we're considering, the situation looks like this:
![\includegraphics[bb = 82 283 513 512, scale=0.6]{fig/F06-reflection.ps}](img223.png)
There are evenly spaced planes (shown as horizontal lines parallel to the plane of reflection) where the two plane waves are in phase, and others where they are exactly out of phase and cancel.
Looking along one of the planes where the phases are aligned (say, right at the wall itself) we see that the waves are apparently elongated; but as we watch the waves ``move" along the wall we'll also be distracted to notice they appear to be moving faster than the speed of sound. (Still, at any location where there is sound present, if we place a microphone we'll pick up the original frequency.)
An important particular case is that n which the incident sound is perpendicular
to the reflecting plane, so that the sound heads directly toward it and is
reflected in exactly the opposite direction it came from. Suppose for
simplicity
that the incident plane wave is traveling in the ![]() direction and it is
reflected off the perpendicular plane
direction and it is
reflected off the perpendicular plane ![]() . The incident and reflected
plane waves are then:
. The incident and reflected
plane waves are then:
![\includegraphics[bb = 14 14 496 472, scale=0.6]{fig/F07-standing-wave.ps}](img230.png)
1. A car is moving toward you at 60 miles per hour. Its horn is blowing at 440 Hz. By how many half tones does the sound rise above 440 Hz because of the car's motion?
2. Suppose the same car has the same horn blowing, but now you hear a pitch of 400 Hz. Assuming the car is moving directly away from you, how fast is it moving (in miles per hour)?
3. A sound has a wavelength of 4 feet. What is its frequency?
4. If two sounds are a perfect fifth apart, what is the ratio of their wavelengths?
5. Suppose that ten feet away from a loudspeaker the SPL is 60 dB. (and that the speaker is the only object making sound nearby). What is the SPL 20 feet away from the loudspeaker?
6. A 440-Hz. sinusoid is traveling in a plane wave in the ![]() direction.
Two microphones are placed at
direction.
Two microphones are placed at ![]() and
and ![]() foot, respectively. What is
the phase difference, in radians, between the signals picked up by the two
microphones?
foot, respectively. What is
the phase difference, in radians, between the signals picked up by the two
microphones?
Project: frequency response of a bandpass filter
This project shows how to measure the frequency response of a filter, whether it's a designed one (as in this case) or it's something that acts as an unintentional filter (such as a loudspeaker that doesn't have a flat frequency response--and, in fact, none of them do.)
The filter we'll measure is the bandpass filter supplied in the music 170 library (called ``bandpass"). It's a classical filter design that appears often in digital audio applications.
To measure it, make a ``sinusoid" object and pass it through a ``bandpass" object. Make two ``meter" objects, and connect one to the output of the oscillator (so that you see what you're inputting to the filter) and one to the filter output so you can see how the two levels differ.
If you want to save time later, you can slightly complicate the patch by inserting a multiplier between the oscillator and its two connections (with a constant to multiply it by) so that you can adjust the oscillator's output to a round number in dB; but this isn't necessary to finish the project.
We're interested in two settings of the filter: the center frequency should be 1000 Hz, and the value of ``Q" set to 10 and to 20. For each of these two filter settings do the following:
Set the oscillator's frequency to a series of values separated from 1000 by half octaves:
31, 44, 62, 88, 125, 176, 250, 353, 500, 707, 1000, 1414, 2000, 2828, 4000, 5656, 8000
With these numbers evenly spaced on the horizontal axis (a logarithmic scale), plot on the vertical axis the gain in decibels (the output level of the filter minus the input level). These numbers will all be negative. (Suggestion: find all the 34 values first--each filter's gain at each of the 17 frequencies shown--so that you will know what the bounds of the graph should be.) Draw two traces, one for each of the two filters. Enjoy the fact that at high frequencies you get two nearly parallel lines. How many decibels per octave do the filters' frequency responses drop off by at frequencies above about 2000?