7. Sound Radiation and Measurement

Because sounds in real air are so different from signals, the things that convert between the two--microphones and speakers--aren't neutral elements that we can ignore but, instead, often have a huge impact on a sound production chain,. Both speakers and microphones come in a bewilderingly complicated array of types, shapes, and sizes, and what is well suited to one task might be ill suited to another.

Of the two, speakers are the more complicated because their greater size means that the spatial anomalies in their output are much greater. Microphones, on the other hand, can often be thought of as sampling sounds at a single point in space. So that's where we will start this chapter.

7.1 Microphones

At a fixed point in space, sound requires four numbers to determine it: the time-varying pressure and a three-component vector that gives the velocity of air at that point. All four are functions of time. (There are other variables such as displacement and acceleration, but these are determined by the velocity.)

Suppose now that there is a sinusoidal plane wave, with peak pressure $a$, traveling in any direction at all. It still passes through the origin since it is defined everywhere. Its pressure at the origin is still the function of time:

$$p(t) = {a} \cos(2 \pi f t)$$

(Once more we're ignoring the initial phase term). The velocity is a vector $v(t)$, whose magnitude we denote by $\vert v(t)\vert$. In a suitably well-behaved gas, this magnitude is equal to:

$$\vert v(t)\vert = {c \over {p_a}} p(t)$$

(Here, $c$ is the speed of sound, as defined in Section 6.3, and $p_a$ is atmospheric pressure, about 101,000 newtons per square meter.)

Now suppose the plane wave is traveling at an angle $\theta$ from the $x$ axis, and that we want to know the velocity component in the $x$ direction. (Knowing this will allow us also to get the velocity components in any other specific direction because we can just orient the coordinate system with $x$ pointing in whatever direction we want to look in.) The situation looks like this:

The desired $x$ component of the velocity is equal to the projection of the vector $v(t)$ onto the $x$ axis which is the magnitude of $v(t)$ multiplied by the cosine of the angle $\theta$:

$${v_x}(t) = \cos(\theta) {c \over {p_a}} p(t)$$

Ideally a microphone measures some linear combination of the pressure $p(t)$ and the three velocity components ${v_x}(t), {v_y}(t), {v_z}(t)$. Whatever combination of the three velocity components we're talking about, we can take to be only a multiple of the $x$ component by suitably choosing a coordinate system so that the microphone is pointing in the negative $x$ direction (so that it picks up the velocity in the positive $x$ direction--microphones always get pointed in the direction the wind is presumed to be coming from). Then the only combinations we can get are of the form

$$a p(t) + b {{p_a} \over c} {v_x}(t)$$

where we can choose the parameters $a$ and $b$ freely. (We took a slight liberty and inserted a term ${{p_a} / c}$ so that $a$ and $b$ have the same normalization.)

Now we consider what happens when a plane wave comes in at various choices of angle $\theta$. If the plane wave is coming in in the positive $x$ direction (directly into the microphone) the $\cos(\theta)$ term equals one, and we plug in the formula for ${v_x}$ to find that the microphone picks up a signal of strength $a+b$. If, on the other hand, the plane wave comes from the opposite direction, the strength is $\vert a-b\vert$. Here are three choices of $a$ and $b$, all arranged so that $a+b=1$ so that they have the same gain in the direction $\theta=0$:

Here are the same three examples, shown as polar plots, so that $\theta$ is shown as the angle from the positive $x$ axis, and the absolute value of the magnitude is the distance from the origin--this is how microphone pickup patterns are most often graphed:

Note that the picture is now turned around so that the mic is now pointing in the positive $x$ direction, in order to make it agree with the convention for graphing microphone pickup patterns. Also, for the example at right, for angles close to $\pi$ the response is negative, but I showed the absolute value to avoid having the curve fold inside itself to avoid confusion.

In the special case where $a=1$ and $b=0$ (i.e. the microphone is sensitive to pressure only and not at all to velocity), there is no dependence on the direction at all. Such a microphone is called omnidirectional. If $a=b=1/2$, so that there is no pickup in the opposite direction ($\theta = \pi$), the microphone is cardioid (named for the shape of the polar plot above). If $b >1/2$ there's still an angle $\theta$ at which there's no pickup, and at greater angles than that the pickup is negative (out of phase). Such a microphone is called hypercardioid. In general, a microphone's pickup gain as a function of angle is called its pickup pattern.

7.2 Radiation From Large Planar Objects

In order to study how vibrating solid objects (such as loudspeakers) radiate sounds into the air, it's best to start with a simple, idealized situation, that of an infinitely large planar surface. The scenario is as pictured:

Supposing that the planar surface is vibrating, sinusoidally, in the direction shown, so that its motion is

$$x(t) = d \cos(2 \pi f t)$$

with the amplitude $d$ in units of distance. On each side of the plane this generates a plane wave moving away from the solid plane. (There's no choice but to emit a plane wave because of the symmetry of the situation; nothing in the setup depends on $y$ or $z$.)

Paying attention to the right-hand side of the plane (the left-hand side acts in the same way but with the sign of $x$ terms in the equations negated), the plane wave has pressure equal to

$$p(x, y, z, t) = a \cos( 2 \pi f (t - x/c))$$

where $a$ is the peak pressure. As we saw in the previous section, the velocity is given by:

$$v(x, y, z, t) = {{c a} \over {p_a}} \cos( 2 \pi f (t - x/c) + \phi)$$

From this we can deduce the physical displacement (by integrating the velocity, or, if you haven't studied calculus, by making arguments based on spinning bicycle wheels):

$$x(x, y, z, t) = {{c a} \over {2 \pi p_a f}} \sin( 2 \pi f (t - x/c) + \phi)$$

This must equal the $x$ position of the solid plane, and so to find the constants $\phi$ and $a$, we equate the two. After some rewriting we get:

$$\phi = \pi/2$$

$$d = {{c a} \over {2 \pi p_a f}}$$

This shows that, to generate a plane wave of a desired amplitude $a$, we have to make the solid plane move physically at an amplitude that depends inversely in frequency. Generating low-frequency sounds requires more physical motion (and hence is harder and more expensive to do) than generating high-frequency ones at the same SPL. In fact, generating a 20 Hz. sound takes 100 times the physical motion that would be required to generate a 2 kHz, one (and consulting of the equal loudness contours, we see that to get an equal loudness the factor rises further yet!) This is why your computer speakers don't do well at low frequencies.

7.3 Radiation From Rectangular Objects: Diffraction

From the preceding section we can predict in general terms that a very large, flat vibrating object will emit a unidirectional beam of sound. This is theoretically true enough, but in our experience sound doesn't move in perfect beams; it's able to round corners. This phenomenon is called diffraction.

Although sound moving in empty space may be described as plane waves, this description breaks down when sound is absorbed or emitted by solid object, and also when it negotiates corners. Typically, higher-frequency sounds (whose wavelengths are shorter) tend to move more in beams, whereas lower-frequency, longer-wavelength ones, are more easily diffracted and can sometimes seem not to move directionally at all.

To study this behavior, we can set up a thought experiment, which comes in two slightly different forms shown below: on the left, sound passing through a rectangular window, and on the right, sound radiating from a rectangular solid plate:

The two situations are similar in that, from the right-hand side of each solid object, we can approximately say that everything we hear was emitted from one point or other on either the hole (in the left-hand-side picture) or on the vibrating solid (on the right). In both situations we're ignoring what happens to the sound on the left-hand side of the object in question: in case of the opening, there will be sound reflected backward from the part of the barrier that isn't missing; and for the vibrating solid, not only is sound radiated on the other (left-hand) side, but in certain conditions, that sound will curve around (diffract!) to the side we're listening on. Later we'll see that we can ignore this if the object is many wavelengths long (at whatever frequency we're considering), but not otherwise.

In either case, we consider that the rectangular surface of interest radiates as if all of its infinitude of points radiated independently and additively. So, to consider what happens at a point in space, we simply trace all possible segments from a point on the surface to our listening point. The diagram below shows two such radiating points, and their effects on two listening points, one nearby, and the other further away:

At faraway listening points, such as the one at right, the distances from all the radiating points are roughly equal (that is, their ratios are nearly one). The RMS amplitude of the radiation is proportional to one over the distance (as we saw in Section 6.2). This region is called the far field. At closer distances (especially at distances smaller than the size of the radiating surface), the distances are much less equal, and nearby points increasingly dominate the sound. In particular, close to the edge of the radiating surface, it's the points at the edge that dominate everything.

In the far field, the amplitude depends on distance as $1/r$, and on direction in a way that we can analyze using this diagram:

For simplicity we've reduced the situation to one spatial dimension (the same thing will happen along the other spatial dimension too.) A segment of length $L$ is radiating a sinusoid of wavelength $\lambda$. We assume that we're listening to the result a large distance away (compared to $L$), at an angle $\theta$ from horizontal (that is, off axis). If $\theta$ is nonzero, the various points along the segment arrive at different times. They're evenly distributed over a time that lasts $L \sin(\theta) / \lambda$ periods; we'll denote this number by $k$.

If $\theta=0$, so that $k=0$ as well, we are listening head on to the radiating surface, all contributing paths arrive with the same delay, and we get the maximum possible amplitude. On the other hand, if $k=1$, we end up summing the signal at relative phases ranging from 0 to $2 \pi$, an entire cycle. A cycle of a sinusoid sums to zero and so there is no sound at all. Assuming $L$ is at least one wavelenth so that $\lambda/L < 1$, the sound forms a beam that spreads at an angle

$$\theta = \sin^{-1} \left ( {{\lambda} \over L} \right )$$

For small values of $\lambda/L$ (i.e., when L is many wavelengths long) the beam spreads at approximately:

$$\theta \approx {{\lambda} \over L}$$

In somewhat more detail, here is what happens when sinusoids f varying frequencies are summed over the fixed length $L \sin(\theta)$:

The only way to get a large sum is to have the wavelength be substantially larger than $L \sin(\theta)$. For smaller wavelengths, for which several cycles fit in the length, even if the number of cycles isn't an integer so that the whole sum doesn't cancel out, there is only a residual amount left after all the complete cycles are left to cancel out (the dark region in the bottom trace above, for example).

If we now consider what happens when we fix $L$ and $\lambda$ (that is, we consider only a fixed frequency), we can compute how the strength of transmission depends on the angle $\theta$. We get the result graphed here:

We get a central ``spot" of maximum amplitude, surrounded by fringes of much smaller amplitude, interleaved with zero crossings at regular intervals. This function recurs often in signal processing (since we often end up summing a signal over a fixed length of time) and it's called the ``sinx" (pronounced ``cinch") function:

$$\mathrm{sinx} (x) = \left \{ \begin{array}{ll} {1} & {x = 0} \ \sin(x) / x & \mbox{otherwise} \end{array} \right .$$

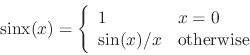
One thing that happens isn't very well explained by this analysis: if what we're talking about is a vibrating rectangle (instead of an opening), some of the radiation actually diffracts all the way around to the other direction. This is, roughly peaking, because the near field is itself limited in size, and so can be thought of as an opening whose radiation is in turn diffracted all over again. In situations where the wavelength of the sound is larger than the object itself, this is in fact the dominant mode of radiation, and everything pretty much spills out in all directions equally.

The dependence of the strength of transmission of sound emitted by an object, depending on angle, is called the object's radiation pattern. In general it depends on frequency, as in the simple example that was worked out here.

7.4 Radiation From Real Objects

Although a few objects in everyday experience radiate sound roughly spherically by injecting air directly into the atmosphere (the end of a sounding air column, for instance, or a firecracker), in practice most objects that make sound do so by vibrating from side to side (for instance, loudspeakers, or the sounding board on a string instrument). Assuming the object is approximately rigid (not a safe assumption at high frequencies but sometimes OK at low ones), the situation is as pictured:

As the object wobbles from side to side (supposing at the moment it is wobbling to the right) it will push air into the atmosphere on its right-hand side (labeled ``+" in the diagram), and suck an equal amount of air back out on its left-hand side (marked ``-").

Denoting the diameter of the object as $L$, we consider two cases. First, at frequencies high enough that the wavelength is much smaller than $L$, sound radiated from the two sides will be at least somewhat directional, so that, listening from the right-hand side of the object, for example, we will hear primarily the influence of the ``+" area. The sound will radiate primarily to the left and right; if we listen from the top or bottom, the two will arrive out of phase and, although in practice they will never cancel each other out, they won't exactly add either. The sound radiated will be at least somewhat directional.

At low frequencies, the sound diffracts so that the radiation pattern is more uniform. At frequencies so low that the wavelength is several times the size $L$, the sound from the ``+" and ``-" regions arrive at phases that differ only by $2L / \lambda$ cycles, and if this is much smaller than one, they will nearly cancel each other out. We conclude that in the far field, vibrating objects are lousy at radiating sounds at wavelengths much longer than themselves.

If we stay in the near field, on the other hand, the ``+" region might be proportionally much closer to us than the ``-" region, so that the cancellation doesn't occur and the low frequencies aren't significantly attenuated. So a microphone placed within less than the diameter of an object tends to pick up low frequencies at higher amplitudes than one placed further away. This is called the proximity effect, although it would perhaps have been better terminology to consider this the natural sound of the object and to give a name to the canceling effect of low-frequency radiation at a distance instead.

Exercises and Project

1. A sinusoidal plane wave at 20 Hz. has an SPL of 80 decibels. What is the RMS displacement (in millimeters.) of air (in other words, how far does the air move)?

2. A rectangular vibrating surface one foot long is vibrating at 2000 Hz. Assuming the speed of sound is 1000 feet per second, at what angle off axis should the beam's amplitude drop to zero?

3. How many dB less does a cardioid microphone pick up from an incoming sound 90 degrees ($\pi/2$ radians) off-axis, compared to a signal coming in frontally (at the angle of highest gain)?

4. Suppose a sound's SPL is 0 dB (i.e., it's about the threshold of hearing at 1 kHz.) What is the total power that you ear receives? (Assume, a bit generously, that the opening is 1 square centimeter).

5. If light moves at $3 \cdot 10^{8}$ meters per second, and if a certain color has a wavelength of 500 nanometers (billionths of a meter - it would look green to human eyes), what is the frequency? Would it be audible if it were a sound? [NOTE: I gave the speed of light incorrectly (mixed up the units, ouch!) - we'll accept answers based on either the right speed or the wrong one I first gave.]

6. A speaker one meter from you is paying a tone at 440 Hz. If you move to a position 2 meters away (and then stop moving), at what pitch to you now hear the tone? (Hint: don't think too hard about this one).

Project: why you really, really shouldn't trust your computer speaker.

We know from project 1 that computer speakers perform badly at low frequencies, sometimes failing to do much of anything below 500 Hz. But within the sweet spot of hearing, 1000 to 2000 Hz, say, are things starting to get normal? On my computer at least, it's impossible to believe anything at all about the audio system, as measured from speaker to microphone.

In this project, you'll measure the speaker-to-microphone gain of your laptop. but instead of looking at a wide range of frequencies, we're interested in a single octave, from 1000 to 2000, in steps of 100 Hz. The patch is somewhat complicated. You'll make a sinusoid to play out the speaker (no problem) but then you'll want to find the level, in dB, of what your microphone picks up. Since it will pick up a lot of other sound besides the sinusoid, you'll need to bandpass filter the input signal from the microphone to (at least approximately) isolate the sinusoid so you can measure it. Here's the block diagram I used:

To use it, set the Q for both bandpass filters to 10. Set the frequency of the sinusoid, and the center frequencies of both filters, to 1000. You should notice that the gain of the filter isn't one - this is why you have to monitor the signal you're sending out the speaker through a matching filter, so that you're measuring the sinusoid's strength the same way on the output as on the input.

Now choosing a reasonable output level, and pushing the input level all the way to 100 (unity gain), verify that you're really measuring the input level in its meter (by turning the output off and on--you should see the level drop by at least about 20 dB when it's off. If not, you might have the filters set wrong, or perhaps Pd is mis-configured and looking for the wrong input.) Also, don't choose an output level so high it distorts the sinusoid - you should be able to hear if this is happening. Most likely an output level from 70 to 80 will be best.

The gain is the difference between the input and output levels (quite possibly negative; that's no problem). Now find the gain (from output to input, via the speaker and microphone) for frequencies 1000, 1100, 1200, ..., 2000 (eleven values). For each value, be sure you've set all three frequencies (the sinusoid and the two filters). Now graph the result, and if you've got less than 15 dB of variation your computer audio system is better than mine.