




Next: Waveshaping using an exponential
Up: Examples
Previous: Waveshaping and difference tones
Contents
Index
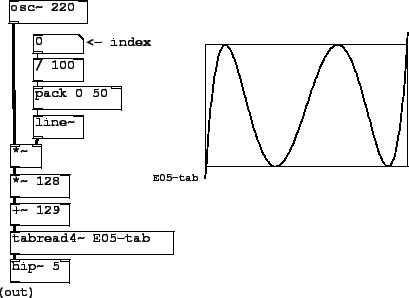
Patch E05.chebychev.pd(Figure 5.12) demonstrates how you can use waveshaping
to generate pure harmonics. We'll limit ourselves to a specific example here;
for all the details see [Leb79]. In this example we would like
to generate the pure fifth harmonic,
Figure 5.12:
Using Chebychev polynomials as waveshaping transfer functions.
 |
by waveshaping a sinusoid
We just
need to find a suitable transfer function 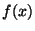 . Our technique is to use
the formula for the waveshaping function
. Our technique is to use
the formula for the waveshaping function 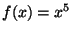 (page
(page ![[*]](file:/usr/share/latex2html/icons/crossref.png) ), which gives first,
third and fifth harmonics; then we add a suitable multiple of
), which gives first,
third and fifth harmonics; then we add a suitable multiple of 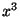 to
cancel the third harmonic, then a multiple of
to
cancel the third harmonic, then a multiple of 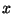 to cancel the first harmonic:
to cancel the first harmonic:
and so we choose
This can be done in the same way to isolate any desired harmonic; the resulting
functions 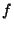 are known as
Chebychev polynomials.
are known as
Chebychev polynomials.
To incorporate this in a waveshaping instrument, we simply build a patch
that works as in Figure 5.5, computing the expression
where ![$p[n]$](img492.png) is a suitable
index
which may vary as a function of the sample number
is a suitable
index
which may vary as a function of the sample number 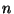 .
.
By suitably combining Chebychev polynomials we can fix any desired
superposition of components in the output waveform. But the real
promise of waveshaping--that by simply changing the index we can
manufacture spectra that evolve in a variety of interesting ways--is
not addressed, at least directly, in the Chebychev picture.





Next: Waveshaping using an exponential
Up: Examples
Previous: Waveshaping and difference tones
Contents
Index
msp
2003-08-09
