




Next: Sinusoidal waveshaping: evenness and
Up: Examples
Previous: Waveshaping using Chebychev polynomials
Contents
Index
We return now to the spectra computed on Page ![[*]](file:/usr/share/latex2html/icons/crossref.png) ,
corresponding to waveshaping functions of the form
,
corresponding to waveshaping functions of the form 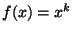 . We note
with pleasure that not only are they all in phase (so that they can
be superposed with easily predictable results) but also that the spectra
spread out increasingly with
. We note
with pleasure that not only are they all in phase (so that they can
be superposed with easily predictable results) but also that the spectra
spread out increasingly with 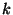 . Also, in a series of the form,
. Also, in a series of the form,
a higher index of modulation will lend more relative weight to the higher
power terms in the expansion; as we saw seen earlier, if the index of
modulation is 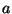 , the terms are
, the terms are 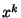 multiplied by
multiplied by 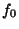 ,
,
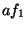 ,
, 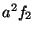 , and so on.
, and so on.
To take the simplest possible example, suppose we wish 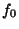 to be the largest
term for
to be the largest
term for 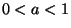 , then for it to be overtaken by the more quickly growing
, then for it to be overtaken by the more quickly growing
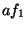 term for
term for 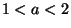 , which is then overtaken by the
, which is then overtaken by the 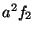 term for
term for
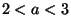 and so on, so that the
and so on, so that the 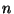 th term takes over at an index equal to
th term takes over at an index equal to 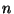 .
To make this happen we just require that
.
To make this happen we just require that
and so fixing 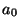 at 1, we get
at 1, we get 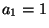 ,
, 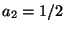 ,
, 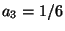 , and in
general,
, and in
general,
These are just the coefficients for the power series for the function
where 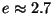 is Euler's constant.
is Euler's constant.
Before plugging in 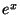 as a transfer function it's wise to plan how we
will deal with signal amplitude, since
as a transfer function it's wise to plan how we
will deal with signal amplitude, since 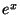 grows quickly as a function of
grows quickly as a function of
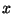 . If we're going to plug in a sinusoid of amplitude
. If we're going to plug in a sinusoid of amplitude 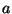 , the maximum output
will be
, the maximum output
will be 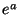 , occuring whenever the phase is zero. A simple and natural
choice is simply to divide by
, occuring whenever the phase is zero. A simple and natural
choice is simply to divide by 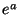 to reduce the peak to one, giving:
to reduce the peak to one, giving:
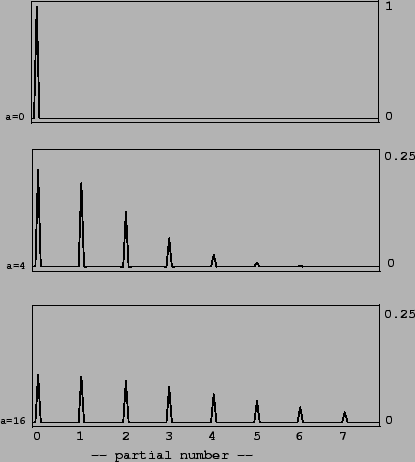
This is realized in Patch E06.exponential.pd. Resulting spectra for
 0, 4, and 16 are shown in Figure 5.13. As the waveshaping index
rises, progressively less energy is present in the fundamental; the energy
is increasingly spread over the partials.
0, 4, and 16 are shown in Figure 5.13. As the waveshaping index
rises, progressively less energy is present in the fundamental; the energy
is increasingly spread over the partials.
Figure 5.13:
Spectra of waveshaping output using an exponential transfer function.
Indices of modulation of 0, 4, and 16 are shown; note the different vertical
scales.
 |





Next: Sinusoidal waveshaping: evenness and
Up: Examples
Previous: Waveshaping using Chebychev polynomials
Contents
Index
msp
2003-08-09
![]() ,
corresponding to waveshaping functions of the form
,
corresponding to waveshaping functions of the form ![]() . We note
with pleasure that not only are they all in phase (so that they can
be superposed with easily predictable results) but also that the spectra
spread out increasingly with
. We note
with pleasure that not only are they all in phase (so that they can
be superposed with easily predictable results) but also that the spectra
spread out increasingly with ![]() . Also, in a series of the form,
. Also, in a series of the form,
![]() to be the largest
term for
to be the largest
term for ![]() , then for it to be overtaken by the more quickly growing
, then for it to be overtaken by the more quickly growing
![]() term for
term for ![]() , which is then overtaken by the
, which is then overtaken by the ![]() term for
term for
![]() and so on, so that the
and so on, so that the ![]() th term takes over at an index equal to
th term takes over at an index equal to ![]() .
To make this happen we just require that
.
To make this happen we just require that
![]() as a transfer function it's wise to plan how we
will deal with signal amplitude, since
as a transfer function it's wise to plan how we
will deal with signal amplitude, since ![]() grows quickly as a function of
grows quickly as a function of
![]() . If we're going to plug in a sinusoid of amplitude
. If we're going to plug in a sinusoid of amplitude ![]() , the maximum output
will be
, the maximum output
will be ![]() , occuring whenever the phase is zero. A simple and natural
choice is simply to divide by
, occuring whenever the phase is zero. A simple and natural
choice is simply to divide by ![]() to reduce the peak to one, giving:
to reduce the peak to one, giving:
