Acoustics of digital audio signals

Digital audio processing--the analysis and/or synthesis of digital sound-is done by processing digital audio signals. These are sequences of numbers,

$$..., x[n-1], x[n], x[n+1], ...$$

where the index $n$, called the sample number, may range over some or all the integers. A single number in the sequence is called a sample. (To prevent confusion we'll avoid the widespread, conflicting use of the word ``sample" to mean ``recorded sound".) Here, for example, is the real sinusoid:

REAL SINUSOID

$$x[n] = a \cos (\omega n + \phi ),$$

where $a$ is the amplitude, $\omega$ the angular frequency, and $\phi$ the initial phase. At sample number $n$, the phase is equal to $\phi + \omega n$.

We call this sinusoid real to distinguish it from the complex sinusoid (chapter ), but where there's no chance of confusion we will simply say ``sinusoid" to speak of the real-valued one.

Figure 1.1 shows a sinusoid graphically.

Figure 1.1: A digital audio signal, showing its discrete-time nature. This one is a REAL SINUSOID, fifty points long, with amplitude 1, angular frequency 0.24, and initial phase zero.

The reason sinusoidal signals play such a key role in audio processing is that, if you shift one of them left or right by any number of samples, you get another one. So it is easy to calculate the effect of all sorts of operations on them. Our ears use this same magic property to help us parse incoming sounds, which is why sinusoidal signals, and combinations of them, can be used for a variety of musical effects.

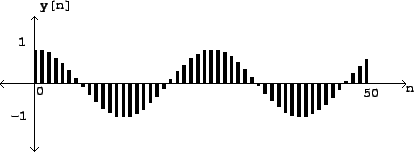Digital audio signals do not have any intrinsic relationship with time, but to listen to them we must choose a sample rate, usually given the variable name $R$, which is the number of samples that fit into a second. Time is related to sample number by $Rt = n$, or $t = n/R$. A sinusoidal signal with angular frequency $\omega$ has a real-time frequency equal to

$$f = {{\omega R} \over {2 \pi}}$$

in cycles per second, because a cycle is $2\pi$ radians and a second is $R$ samples.

A real-world audio signal's amplitude might be expressed as a time-varying voltage or air pressure, but the samples of a digital audio signal are unitless real (or in some later chapters, complex) numbers. We'll casually assume here that there is ample numerical accuracy that round-off errors are negligible, and that the numerical format is unlimited in range, so that samples may take any value we wish. However, most digital audio hardware works only over a fixed range of input and output values. We'll assume that this range is from -1 to 1. Modern digital audio processing software usually uses a floating-point representation for signals, so that the may assume whatever units are convenient for any given task, as long as the final audio output is within the hardware's range.